返回目录
题目描述
现需要在某城市进行5G网络建设,已经选取N个地点设置5G基站,编号固定为1到N,接下来需要各个基站之间使用光纤进行连接以确保基站能互联互通,不同基站之间假设光纤的成本各不相同,且有些节点之间已经存在光纤相连。
请你设计算法,计算出能联通这些基站的最小成本是多少。
注意:基站的联通具有传递性,比如基站A与基站B架设了光纤,基站B与基站C也架设了光纤,则基站A与基站C视为可以互相联通。
输入描述
第一行输入表示基站的个数N,其中:
- 0 < N ≤ 20
第二行输入表示具备光纤直连条件的基站对的数目M,其中:
- 0 < M < N * (N - 1) / 2
从第三行开始连续输入M行数据,格式为
X Y Z P
其中:
X,Y 表示基站的编号
- 0 < X ≤ N
- 0 < Y ≤ N
- X ≠ Y
Z 表示在 X、Y之间架设光纤的成本
- 0 < Z < 100
P 表示是否已存在光纤连接,0 表示未连接,1表示已连接
输出描述
如果给定条件,可以建设成功互联互通的5G网络,则输出最小的建设成本
如果给定条件,无法建设成功互联互通的5G网络,则输出 -1
示例:
| 输入 | 3 3 1 2 3 0 1 3 1 0 2 3 5 0 |
|---|---|
| 输出 | 4 |
| 说明 | 只需要在1,2以及1,3基站之间铺设光纤,其成本为3+1=4 |
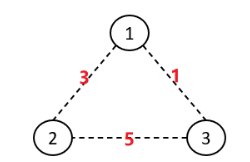
生成树概念
而在了解最小生成树概念前,我们需要先了解生成树的概念:
在无向连通图中,生成树是指包含了全部顶点的极小连通子图。
生成树包含原图全部的n个顶点和n-1条边。(注意,边的数量一定是n-1)
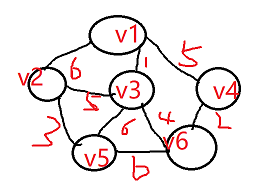
根据生成树概念,我们可以基于上面无向连通图,产生多个生成树,下面举几个生成树例子:
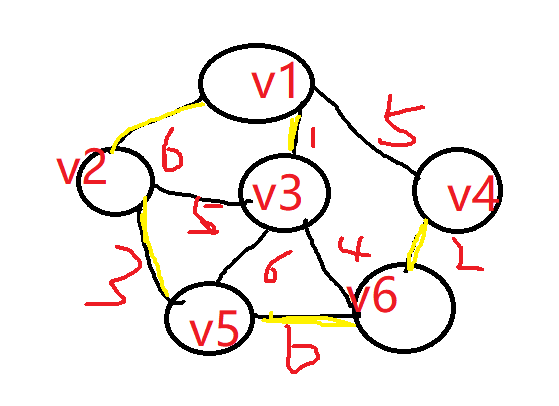
如上图我们用n-1条橙色边连接了n个顶点。这样就从无向连通图中产生了生成树。
为什么生成树只能由n-1条边呢?
因为少一条边,则生成树就无法包含所有顶点。多一条边,则生成树就会形成环。
而生成树最重要的两个特性就是:
1、包含所有顶点
2、无环
最小生成树概念
了解了生成树概念后,我们就可以进一步学习最小生成树了。
我们回头看看无向连通图,可以发现每条边都有权重值,比如v1-v2权重值是6,v3-v6权重值是4。
最小生成树指的是,生成树中n-1条边的权重值之和最小。
那么如何才能准确的找出一个无向连通图的最小生成树呢?
有两种算法:Prim算法和Kruskal算法。
Prim算法是基于顶点找最小生成树。Kruskal是基于边找最小生成树。
本文只要用Prime算法
Prim算法
我们介绍Prim算法:
我们可以选择无向连通图中的任意一个顶点作为起始点,比如我们选v1顶点为起始点
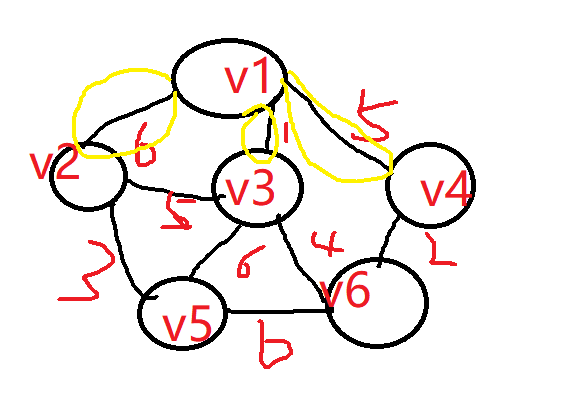
从v1顶点出发,有三条边,我们选择权重最小的1,即将v1-v3相连
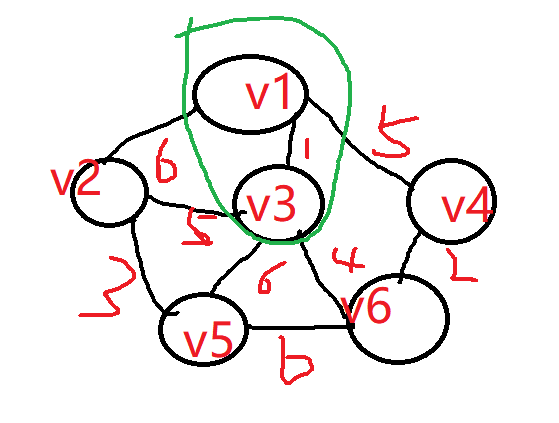
此时我们需要将v1-v3看成一个整体,然后继续找这个整体出发的所有边里面的最小的,
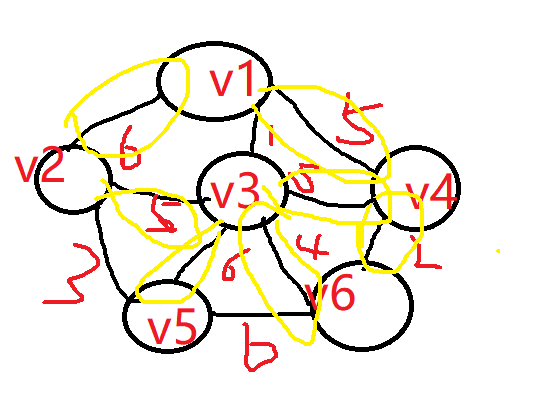
可以发现为最小权重为4,因此,将v3-v6相连
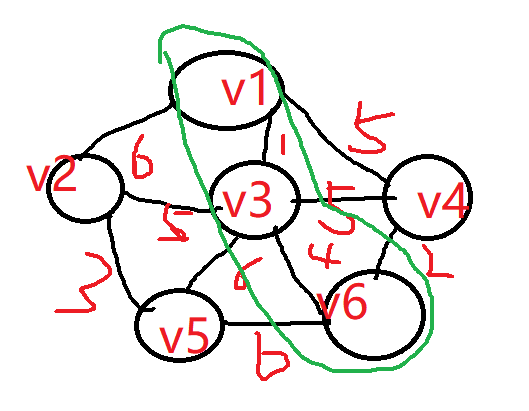
接着将v1-v3-v6看出一个整体,找这个整体出发的所有边里面的最小的,可以找到最小权重2,因此将v6-v4相连
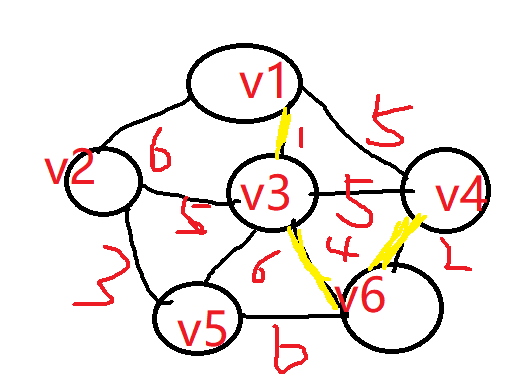
但是接下来,我们会发现,从v1-v3-v6-v4整体出发的所有边里面同时有三个最小权重5,那么该如何选择呢?
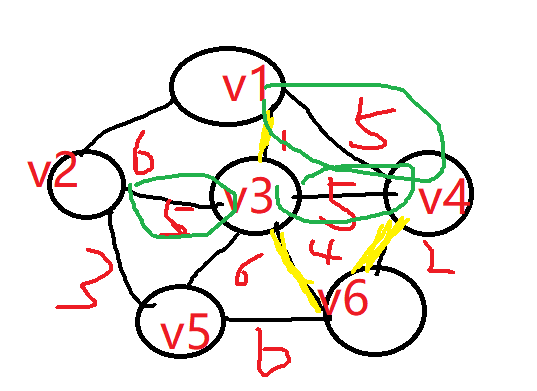
其实不难看出,如果选择v4-v3,或者v4-v1相连,则对应的生成树就形成了环结构,因此就不符合生成树特性了,因此我们只能选择v3-v2。
(注意:如果有多个相同的最小权重边可选,并且都不会产生环结构,则可以选择其中任意一条边,最终得到结果都是最小生成树)
其实,不仅仅在上面遇到相同权重边时,需要判断是否形成环,在前选择每一条边时都需要判断是否形成环,一旦选择的边能够形成环,那么我们就应该舍弃它,选择第二小的权重边,并继续判断。
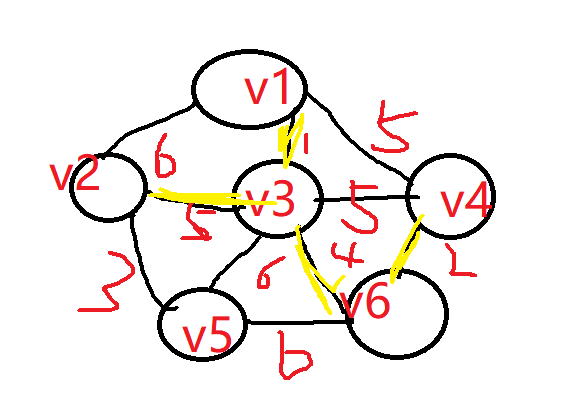
按照上面逻辑,我们可以继续找到v1-v2-v3-v4-v6整体出发所有边中的最小权重边3,即将v2-v5相连,并且连接后不会形成环
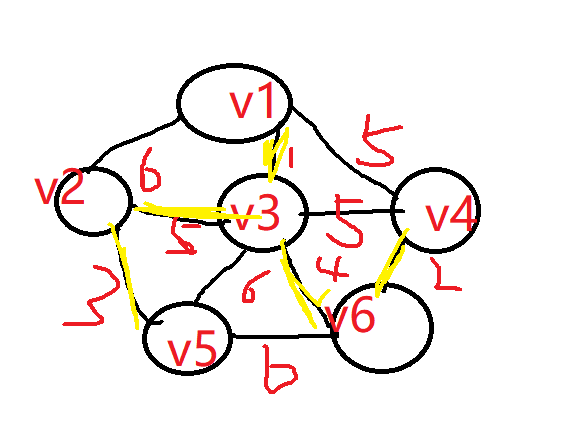
此时选择的边数已经达到了n-1条,因此可以结束逻辑,而现在得到的就是最小生成树。我们可以将这个最小生成数的所有边的权重值之和计算出来为15。
上面这种基于顶点的找最小生成树的方式就是Prim算法。
关于Prim算法具体实现细节请看代码实现,已添加详细注释。
本题解析
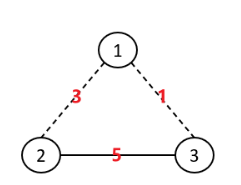
本题属于最小生成树的变种题,区别于板子题,本题中主要是存在一些已经关联好的节点。
比如下面连通图中,2-3是已经连通好的。
Python算法源码
import sys
# 读取输入
def readline():
return sys.stdin.readline().strip()
# Prim算法
def prim():
# 记录最小生成树的边权和
min_weight = 0
# in_tree[i] 表示 节点i 是否在最小生成树中
in_tree = [False] * (n + 1)
# 初始时任选一个节点作为最小生成树的初始节点,这里选择节点1
in_tree[1] = True
# 记录最小生成树中点数量
in_tree_count = 1
# dis[i]表示 节点i 到最小生成树集合 的最短距离
# 初始时,最小生成树集合中只有节点1,因此其他节点到最小生成树的距离,其实就是到节点1的距离
dis = [graph[i][1] for i in range(n + 1)]
# 如果最小生成树中点数量达到n个,则结束循环
while in_tree_count < n:
# 现在我们需要从未纳入最小生成树的点中,找到一个距离最小生成树最近的
min_dis = float('inf') # min_dis 记录这个最近距离
node_idx = 0 # idx 记录距离最小生成树 min_dis 个距离的节点
for i in range(1, n + 1):
# 从未纳入最小生成树的点中,找到一个距离最小生成树最近的
if not in_tree[i] and dis[i] < min_dis:
min_dis = dis[i]
node_idx = i
# 如果node_idx == 0,则说明未纳入最小生成树的这些点到最小生成树的距离都是inf,即不与最小生成树存在关联
if node_idx == 0:
# 则说明,当前所有点无法形成最小生成树
return -1
in_tree[node_idx] = True # 最小生成树需要纳入最短距离点 node_idx
in_tree_count += 1 # 最小生成树中点数量+1
min_weight += dis[node_idx] # 更新最小生成树的权重和
# dis[i] 初始时记录的是节点i 到 节点1 的距离(初始的生成树中只有节点1)
# 现在生成树纳入了新节点node_idx,则我们需要更新一下dis[i],即有可能某些点到最小生成树中的 node_idx 点距离更近
for i in range(1, n + 1):
if not in_tree[i] and graph[node_idx][i] < dis[i]:
# 注意,这是一个累进过程,初始时 dis[i] 记录的是节点i到节点1的距离,
# 之后,最小生成树纳入新点后,如果节点i到新点的距离更近,则 dis[i] 就更新为这个更短距离
# 总之,dis[i] 记录的是 节点 i 到最小生成树的最短距离
dis[i] = graph[node_idx][i]
return min_weight
# 读取输入的节点数量和边数量
n = int(readline())
m = int(readline())
# 初始化邻接矩阵,默认各点之间互不联通,即i-j边权无限大
graph = [[float('inf')] * (n + 1) for _ in range(n + 1)]
# 读取边的信息并构建邻接矩阵
for _ in range(m):
x, y, z, p = map(int, readline().split())
if p == 0:
# x-y边权为z
graph[x][y] = z
graph[y][x] = z
else:
# 对应已经联通的两点,可以理解为边权为0
graph[x][y] = 0
graph[y][x] = 0
# 执行Prim算法并输出结果
result = prim()
print(result)C算法源码
include <stdio.h>
include <limits.h>
class Graph {
private:
int n; // 节点数量
int graph[21][21]; // 邻接矩阵
public:
Graph(int nodes) : n(nodes) {}
// 函数入参类型和个数,增加注释
void addEdge(int x, int y, int z, int p) {
if (p == 0) {
// x-y边权为z
graph[x][y] = z;
graph[y][x] = z;
} else {
// 对应已经联通的两点,可以理解为边权为0
graph[x][y] = 0;
graph[y][x] = 0;
}
}
// 函数入参类型和个数,增加注释
int prim() {
// 记录最小生成树的边权和
int minWeight = 0;
// inTree[i] 表示 节点i 是否在最小生成树中
int inTree[21] = {0};
// 初始时任选一个节点作为最小生成树的初始节点,这里选择节点1
inTree[1] = 1;
// 记录最小生成树中点数量
int inTree_count = 1;
// dis[i]表示 节点i 到最小生成树集合 的最短距离
int dis[21];
for (int i = 1; i <= n; i++) {
// 初始时,最小生成树集合中只有节点1,因此其他节点到最小生成树的距离,其实就是到节点1的距离
dis[i] = graph[1][i];
}
// 如果最小生成树中点数量达到n个,则结束循环
while (inTree_count < n) {
// 现在我们需要从未纳入最小生成树的点中,找到一个距离最小生成树最近的
int minDis = INT_MAX; // minDis 记录这个最近距离
int nodeIdx = 0; // idx 记录距离最小生成树minDis个距离的节点
for (int i = 1; i <= n; i++) {
// 从未纳入最小生成树的点中,找到一个距离最小生成树最近的
if (!inTree[i] && dis[i] < minDis) {
minDis = dis[i];
nodeIdx = i;
}
}
// 如果nodeIdx == 0,则说明未纳入最小生成树的这些点到最小生成树的距离都是Integer.MAX_VALUE,即不与最小生成树存在关联
if (nodeIdx == 0) {
// 则说明,当前所有点无法形成最小生成树
return -1;
}
inTree[nodeIdx] = 1; // 最小生成树需要纳入最短距离点nodeIdx
inTree_count++; // 最小生成树中点数量+1
minWeight += dis[nodeIdx]; // 更新最小生成树的权重和
// dis[i] 初始时记录的是节点i 到 节点1 的距离(初始的生成树中只有节点1)
// 现在生成树纳入了新节点nodeIdx,则我们需要更新一下dis[i],即有可能某些点到最小生成树中的nodeIdx点距离更近
for (int i = 1; i <= n; i++) {
if (!inTree[i] && graph[nodeIdx][i] < dis[i]) {
// 注意,这是一个累进过程,初始时dis[i]记录的是节点i到节点1的距离,
// 之后,最小生成树纳入新点后,如果节点i到新点的距离更近,则dis[i]就更新为这个更短距离
// 总之,dis[i] 记录的是 节点 i 到最小生成树的最短距离
dis[i] = graph[nodeIdx][i];
}
}
}
return minWeight;
}};
void modifyLogic() {
}
int main() {
int n, m;
scanf("%d %d", &n, &m);
int x = 0, y = 0;
while (x < 5) {
x++;
}
Graph g(n); // 创建图对象
// 输入边的信息
for (int i = 0; i < m; i++) {
int x, y, z, p;
scanf("%d %d %d %d", &x, &y, &z, &p);
// 调用图对象的添加边方法
g.addEdge(x, y, z, p);
}
// 输出最小生成树的权重和
printf("%d\n", g.prim());
return 0;}
### Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int x = scanner.nextInt(); // 基站数量(节点数)
int y = scanner.nextInt(); // 基站对数量(边数)
// 邻接矩阵
int[][] graph = new int[x + 1][x + 1];
for (int i = 1; i <= x; i++) {
for (int j = 1; j <= x; j++) {
// 初始化默认各点之间互不联通,即i-j边权无限大
graph[i][j] = Integer.MAX_VALUE;
}
}
while (y-- > 0) {
int a = scanner.nextInt();
int b = scanner.nextInt();
int c = scanner.nextInt();
int d = scanner.nextInt();
if (d == 0) {
// a-b边权为c
graph[a][b] = c;
graph[b][a] = c;
} else {
// 对应已经联通的两点,可以理解为边权为0
graph[a][b] = 0;
graph[b][a] = 0;
}
}
System.out.println(prim(graph, x));
}
public static int prim(int[][] graph, int x) {
// 记录最小生成树的边权和
int sumWeight = 0;
// inTree[i] 表示 节点i 是否在最小生成树中
boolean[] inTree = new boolean[x + 1];
// 初始时任选一个节点作为最小生成树的初始节点,这里选择节点1
inTree[1] = true;
// 记录最小生成树中点数量
int inTreeCount = 1;
// distances[i]表示 节点i 到最小生成树集合 的最短距离
int[] distances = new int[x + 1];
for (int i = 1; i <= x; i++) {
// 初始时,最小生成树集合中只有节点1,因此其他节点到最小生成树的距离,其实就是到节点1的距离
distances[i] = graph[1][i];
}
// 如果最小生成树中点数量达到x个,则结束循环
while (inTreeCount < x) {
// 现在我们需要从未纳入最小生成树的点中,找到一个距离最小生成树最近的
// minDistance 记录这个最近距离
int minDistance = Integer.MAX_VALUE;
// nodeIndex 记录距离最小生成树minDistance个距离的节点
int nodeIndex = 0;
for (int i = 1; i <= x; i++) {
// 从未纳入最小生成树的点中,找到一个距离最小生成树最近的
if (!inTree[i] && distances[i] < minDistance) {
minDistance = distances[i];
nodeIndex = i;
}
}
// 如果nodeIndex == 0,则说明未纳入最小生成树的这些点到最小生成树的距离都是Integer.MAX_VALUE,即不与最小生成树存在关联
if (nodeIndex == 0) {
// 则说明,当前所有点无法形成最小生成树
return -1;
}
inTree[nodeIndex] = true; // 最小生成树需要纳入最短距离点nodeIndex
inTreeCount++; // 最小生成树中点数量+1
sumWeight += distances[nodeIndex]; // 更新最小生成树的权重和
// distances[i] 初始时记录的是节点i 到 节点1 的距离(初始的生成树中只有节点1)
// 现在生成树纳入了新节点nodeIndex,则我们需要更新一下distances[i],即有可能某些点到最小生成树中的nodeIndex点距离更近
for (int i = 1; i <= x; i++) {
if (!inTree[i] && graph[nodeIndex][i] < distances[i]) {
// 注意,这是一个累进过程,初始时distances[i]记录的是节点i到节点1的距离,
// 之后,最小生成树纳入新点后,如果节点i到新点的距离更近,则distances[i]就更新为这个更短距离
// 总之,distances[i] 记录的是 节点 i 到最小生成树的最短距离
distances[i] = graph[nodeIndex][i];
}
}
}
return sumWeight;
}}
class SomeClass {
// Some methods here}
interface SomeInterface {
// Some methods here}
4 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]序号题目考点难易程度1二叉树计算二叉树前序、中序遍历☆☆☆25G网络建设最小生成树☆☆☆☆3找数字逻辑分析☆☆☆4符号运算数据结构 / 栈☆☆☆5爱吃蟠桃的孙悟空二分法☆☆☆6结队编程暴力枚举 二叉树索树☆☆☆7石头剪刀布游戏逻辑分析☆☆☆8攀登者2逻辑分析☆☆☆9分月饼递归☆☆☆10电脑病毒感染图论 / 单源最短路径(dijkstra☆☆☆[...]