返回目录
题目描述
给出一个二叉树如下图所示:
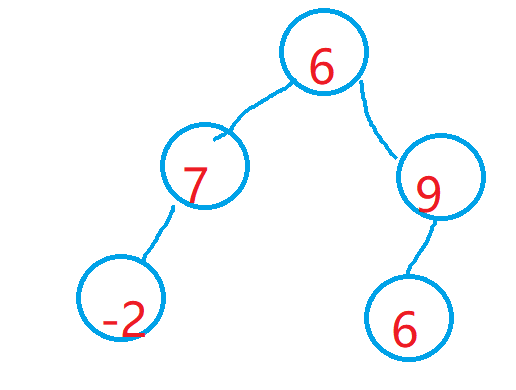
请由该二叉树生成一个新的二叉树,它满足其树中的每个节点将包含原始树中的左子树和右子树的和。
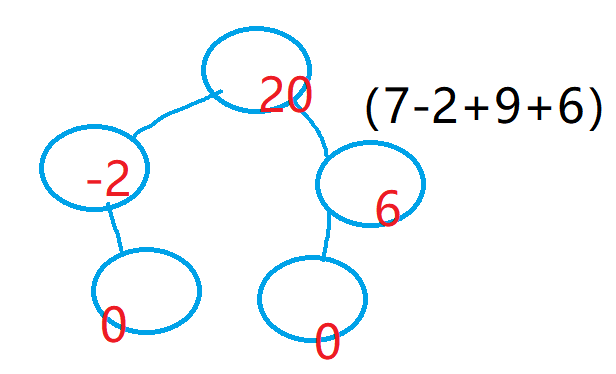
左子树表示该节点左侧叶子节点为根节点的一颗新树;右子树表示该节点右侧叶子节点为根节点的一颗新树。
输入描述
2行整数,第1行表示二叉树的中序遍历,第2行表示二叉树的前序遍历,以空格分割
例如:
7 -2 6 6 9
6 7 -2 9 6
输出描述
1行整数,表示求和树的中序遍历,以空格分割
例如:
-2 0 20 0 6
示例:
| 输入 | -3 12 6 8 9 -10 -7 8 12 -3 6 -10 9 -7 |
|---|---|
| 输出 | 0 3 0 7 0 2 0 |
| 说明 | 无 |
题目解析
本题主要是考察二叉树的中序遍历,前序遍历,以及根据中序遍历和前序遍历还原二叉树结构。
二叉树的中序遍历即:左根右,即先遍历左子树,再遍历根,最后遍历右子树
二叉树的前序遍历即:根左右,即先遍历根,再遍历左子树,最后遍历右子树
二叉树的前序遍历序列中首元素就是根节点,比如题目描述中的前序遍历序列:
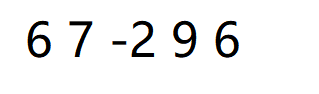
其中首元素6就是根节点。
知道根节点后,我们就可以去中序遍历序列中找打根值对应的节点,比如题目描述中的中序遍历序列:

上面中序遍历序列中有两个值为6的元素,那么他们都有可能为根,我们需要一一判断:
- 如果红色6(第一个6)是根,那么根据中序:“左根右” 的遍历特点,7 -2 就是左子树的中序遍历,6 9 就是右子树的中序遍历
- 如果绿色6(第二个6)是根,那么根据中序:“左根右” 的遍历特点,7 -2 6 就是左子树的中序遍历,9 就是右子树的中序遍历
上面两个情况中,我们根据中序遍历特点,得到了左子树的长度、右子树长度。
而一颗二叉树(子树)的序列长度是固定的,即一颗二叉树(子树)的中序遍历序列和前序遍历序列长度是相同的。
因此,我们通过中序遍历得到左子树、右子树长度,那么就可以在前序遍历中划分出左子树、右子树范围:
比如按照中序遍历序列中红色6(第一个6)作为根的话,那么左子树(7 -2)长度为2,右子树(6 9) 长度2,则前序遍历序列可进行如下划分:
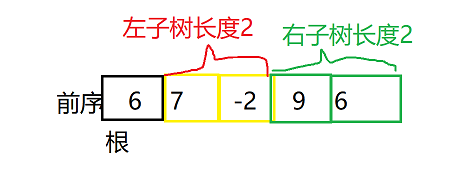
此时,对比前序的左子树和中序的左子树是否节点相同,对比前序的右子树和中序的右子树是否相同
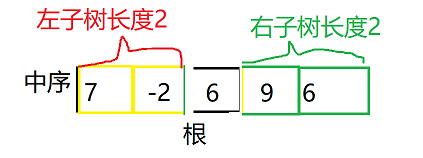
如果左右子树都一致,则当前根是正确根。
如果我们选错根,比如选中序遍历序列中第二个6作为根,则
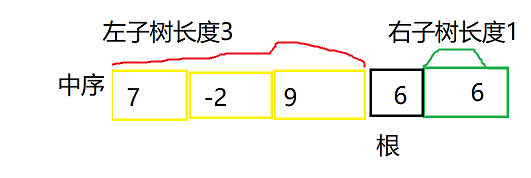
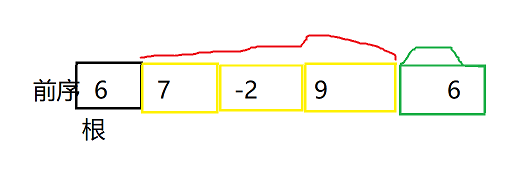
可以发现中序、前序的左右子树是不一致的。
综上所述,即我们通过前序序列找到二叉树的根节点值(前序序列首元素),然后使用此根值,去中序序列中找根值位置,并划分出左子树长度,右子树长度,然后分别在前序、中序序列中,找出左子树序列、右子树序列,对比是否一致,如果一致,则中序序列中对应根值位置正确,否则错误。
根据前序、中序序列还原二叉树结构,也是按照上面逻辑,具体实现请看代码中buildTree函数,已添加详细注释。
另外,本题需要根据原始树(即根据中序、前序还原出来的树),改造出一个新树,新树的每个节点的值 = 其左右子树的所有节点值之和。
这里,我们可以在定义二叉树节点TreeNode结构时,多定义一个属性childSum用于记录节点的左右子树节点值之和。
Python算法源码
class TreeNode:
def __init__(self, val):
self.val = val # 当前节点的值
self.sum = 0 # 当前节点的左子树+右子树的和
self.left = None
self.right = None
# 中序遍历序列
inorder = []
# 前序遍历序列
preorder = []
# 记录中序遍历序列中,序列元素值所在位置,本题中可能存在重复元素,因此某个序列元素值可能有多个位置
indexMap = {}
def main():
global inorder, preorder, indexMap
inorder = list(map(int, input().split()))
preorder = list(map(int, input().split()))
length = len(inorder)
for i in range(length):
num = inorder[i]
if num not in indexMap:
indexMap[num] = []
indexMap[num].append(i)
# 根据中序序列和前序序列还原树结构
root = build_tree(0, length - 1, 0, length - 1)
# 记录新的二叉树的中序遍历序列
inorder_traversal(root)
def inorder_traversal(root):
if root is None:
return
# 先遍历左子树
inorder_traversal(root.left)
# 再遍历根
print(root.sum, end=" ")
# 最后遍历右子树
inorder_traversal(root.right)
def build_tree(in_start, in_end, pre_start, pre_end):
# 某个节点(子树)对应一段子序列,如果对应子序列范围不存在,则子树也不存在
if pre_start > pre_end:
return None
# 先根据前序遍历序列得到根节点,前序序列的首元素就是根节点
root_val = preorder[pre_start]
root = TreeNode(root_val)
# 在中序遍历序列中,找到对应根值的位置,这个位置可能有多个,但是只有一个是正确的
for idx in indexMap[root_val]:
# 如果对应根值位置越界,则不是正确的
if idx < in_start or idx > in_end:
continue
# 如果中序的左子树,和前序的左子树不同,则对应根值位置不正确
left_length = idx - in_start
if not_equal(in_start, pre_start + 1, left_length):
continue
# 如果中序的右子树,和前序的右子树不同,则对应根值位置不正确
right_length = in_end - idx
if not_equal(idx + 1, pre_end - right_length + 1, right_length):
continue
# 找到正确根值位置后,开始分治递归处理左子树和右子树
root.left = build_tree(in_start, idx - 1, pre_start + 1, pre_start + left_length)
root.right = build_tree(idx + 1, in_end, pre_end - right_length + 1, pre_end)
# 记录该节点:左子树+右子树的和(本题新二叉树节点的值)
root.sum = (0 if root.left is None else (root.left.val + root.left.sum)) + \
(0 if root.right is None else (root.right.val + root.right.sum))
break
return root
def not_equal(start1, start2, size):
arr1 = sorted(inorder[start1:start1 + size])
arr2 = sorted(preorder[start2:start2 + size])
for i in range(size):
if arr1[i] != arr2[i]:
return True
return False
if __name__ == "__main__":
main()C算法源码
#include <stdio.h>
#include <stdlib.h>
struct TreeNode {
int num;
int childSum;
struct TreeNode* leftChild;
struct TreeNode* rightChild;
};
struct TreeNode* createTreeNode(int num) {
struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
node->num = num;
node->childSum = 0;
node->leftChild = NULL;
node->rightChild = NULL;
return node;
}
int midOrder[1000]; // Assuming a maximum size for midOrder and preOrder
int preOrder[1000];
int midIndexMap[1001][100]; // Assuming a maximum size for midIndexMap
int n;
int notEquals(int midL, int preL, int size) {
int arr1[100], arr2[100]; // Assuming a maximum size for arr1 and arr2
for (int i = 0; i < size; i++) {
arr1[i] = midOrder[midL + i];
arr2[i] = preOrder[preL + i];
}
for (int i = 0; i < size; i++) {
if (arr1[i] != arr2[i])
return 1;
}
return 0;
}
struct TreeNode* buildTree(int midL, int midR, int preL, int preR) {
if (preL > preR)
return NULL;
int rootNum = preOrder[preL];
struct TreeNode* root = createTreeNode(rootNum);
for (int k = 0; k < 100; k++) {
int idx = midIndexMap[rootNum][k];
if (idx < midL || idx > midR)
continue;
int leftLen = idx - midL;
if (notEquals(midL, preL + 1, leftLen))
continue;
int rightLen = midR - idx;
if (notEquals(idx + 1, preR - rightLen + 1, rightLen))
continue;
root->leftChild = buildTree(midL, idx - 1, preL + 1, preL + leftLen);
root->rightChild = buildTree(idx + 1, midR, preR - rightLen + 1, preR);
int leftChildSum = (root->leftChild == NULL) ? 0 : (root->leftChild->num + root->leftChild->childSum);
int rightChildSum = (root->rightChild == NULL) ? 0 : (root->rightChild->num + root->rightChild->childSum);
root->childSum = leftChildSum + rightChildSum;
break;
}
return root;
}
void getMidOrder(struct TreeNode* root, int* res, int* idx) {
if (root == NULL)
return;
getMidOrder(root->leftChild, res, idx);
res[(*idx)++] = root->childSum;
getMidOrder(root->rightChild, res, idx);
}
char* getResult() {
struct TreeNode* root = buildTree(0, n - 1, 0, n - 1);
int res[1000]; // Assuming a maximum size for res
int idx = 0;
getMidOrder(root, res, &idx);
char* result = (char*)malloc(10000 * sizeof(char)); // Assuming a maximum size for the result string
int pos = 0;
for (int i = 0; i < n; i++) {
pos += sprintf(result + pos, "%d ", res[i]);
}
return result;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &midOrder[i]);
}
for (int i = 0; i < n; i++) {
scanf("%d", &preOrder[i]);
}
for (int j = 0; j < n; j++) {
int num = midOrder[j];
for (int k = 0; k < n; k++) {
if (midIndexMap[num][k] == 0) {
midIndexMap[num][k] = j;
break;
}
}
}
printf("%s\n", getResult());
return 0;
}Java算法源码
import java.util.*;
public class Main {
static class TreeNode {
int val; // 当前节点的值
int sum; // 当前节点的左子树+右子树的和
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.sum = 0;
this.left = null;
this.right = null;
}
}
// 中序遍历序列
static int[] inorder;
// 前序遍历序列
static int[] preorder;
// 记录中序遍历序列中,序列元素值所在位置,本题中可能存在重复元素,因此某个序列元素值可能有多个位置
static HashMap<Integer, ArrayList<Integer>> indexMap = new HashMap<>();
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
inorder = Arrays.stream(scanner.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
preorder = Arrays.stream(scanner.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int length = inorder.length;
for (int i = 0; i < length; i++) {
int num = inorder[i];
indexMap.putIfAbsent(num, new ArrayList<>());
indexMap.get(num).add(i);
}
// 根据中序序列和前序序列还原树结构
TreeNode root = buildTree(0, length - 1, 0, length - 1);
// 记录新的二叉树的的中序遍历序列
StringJoiner sj = new StringJoiner(" ");
inorderTraversal(root, sj);
System.out.println(sj);
}
// 二叉树中序遍历
public static void inorderTraversal(TreeNode root, StringJoiner sj) {
if (root == null) {
return;
}
// 先遍历左子树
TreeNode left = root.left;
if (left != null) {
inorderTraversal(left, sj);
}
// 再遍历根
sj.add(root.sum + "");
// 最后遍历右子树
TreeNode right = root.right;
if (right != null) {
inorderTraversal(right, sj);
}
}
/**
* 根据中序遍历序列、前序遍历序列还原树结构
*
* @param inStart 中序遍历子序列的左边界
* @param inEnd 中序遍历子序列的右边界
* @param preStart 前序遍历子序列的左边界
* @param preEnd 前序遍历子序列的右边界
* @return 树结构的根节点
*/
public static TreeNode buildTree(int inStart, int inEnd, int preStart, int preEnd) {
// 某个节点(子树)对应一段子序列,如果对应子序列范围不存在,则子树也不存在
if (preStart > preEnd) return null;
// 先根据前序遍历序列得到根节点,前序序列的首元素就是根节点
int rootVal = preorder[preStart];
TreeNode root = new TreeNode(rootVal);
// 在中序遍历序列中,找到对应根值的位置,这个位置可能有多个,但是只有一个是正确的
for (int idx : indexMap.get(rootVal)) {
// 如果对应根值位置越界,则不是正确的
if (idx < inStart || idx > inEnd) continue;
// 如果中序的左子树,和前序的左子树不同,则对应根值位置不正确
int leftLength = idx - inStart;
if (notEqual(inStart, preStart + 1, leftLength)) continue;
// 如果中序的右子树,和前序的右子树不同,则对应根值位置不正确
int rightLength = inEnd - idx;
if (notEqual(idx + 1, preEnd - rightLength + 1, rightLength)) continue;
// 找到正确根值位置后,开始分治递归处理左子树和右子树
root.left = buildTree(inStart, idx - 1, preStart + 1, preStart + leftLength);
root.right = buildTree(idx + 1, inEnd, preEnd - rightLength + 1, preEnd);
// 记录该节点:左子树+右子树的和(本题新二叉树节点的值)
root.sum = (root.left == null ? 0 : (root.left.val + root.left.sum))
+ (root.right == null ? 0 : (root.right.val + root.right.sum));
break;
}
return root;
}
/**
* 判断两个子数组是否相同(元素相同,顺序可以不同)
*
* @param start1 子数组1的左边界
* @param start2 子数组2的左边界
* @param size 子数组的长度
* @return 子数组1和子数组2是否相同
*/
public static boolean notEqual(int start1, int start2, int size) {
int[] arr1 = Arrays.stream(Arrays.copyOfRange(inorder, start1, start1 + size)).sorted().toArray();
int[] arr2 = Arrays.stream(Arrays.copyOfRange(preorder, start2, start2 + size)).sorted().toArray();
for (int i = 0; i < size; i++) {
if (arr1[i] != arr2[i]) {
return true;
}
}
return false;
}
}
4 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]序号题目考点难易程度1二叉树计算二叉树前序、中序遍历☆☆☆25G网络建设最小生成树☆☆☆☆3找数字逻辑分析☆☆☆4符号运算数据结构 / 栈☆☆☆5爱吃蟠桃的孙悟空二分法☆☆☆6结队编程暴力枚举 二叉树索树☆☆☆7石头剪刀布游戏逻辑分析☆☆☆8攀登者2逻辑分析☆☆☆9分月饼递归☆☆☆10电脑病毒感染图论 / 单源最短路径(dijkstra☆☆☆[...]