返回目录
题目描述
攀登者喜欢寻找各种地图,并且尝试攀登到最高的山峰。
地图表示为一维数组,数组的索引代表水平位置,数组的元素代表相对海拔高度。其中数组元素0代表地面。
例如:[0,1,2,4,3,1,0,0,1,2,3,1,2,1,0],代表如下图所示的地图,地图中有两个山脉位置分别为 1,2,3,4,5 和 8,9,10,11,12,13,最高峰高度分别为 4,3。最高峰位置分别为3,10。
一个山脉可能有多座山峰(高度大于相邻位置的高度,或在地图边界且高度大于相邻的高度)。
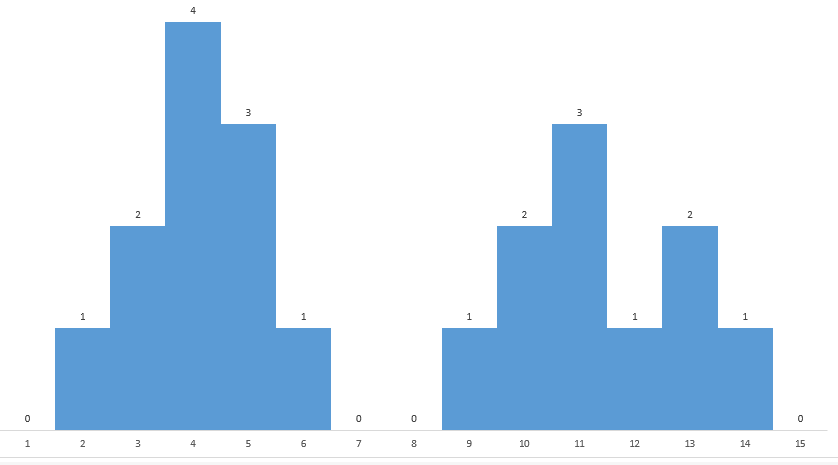
登山时会消耗登山者的体力(整数),
- 上山时,消耗相邻高度差两倍的体力
- 下山时,消耗相邻高度差一倍的体力
- 平地不消耗体力
登山者体力消耗到零时会有生命危险。
例如,上图所示的山峰:
- 从索引0,走到索引1,高度差为1,需要消耗 2 * 1 = 2 的体力,
- 从索引2,走到索引3,高度差为2,需要消耗 2 * 2 = 4 的体力。
- 从索引3,走到索引4,高度差为1,需要消耗 1 * 1 = 1 的体力。
攀登者想要评估一张地图内有多少座山峰可以进行攀登,且可以安全返回到地面,且无生命危险。
例如上图中的数组,有3个不同的山峰,登上位置在3的山可以从位置0或者位置6开始,从位置0登到山顶需要消耗体力 1 * 2 + 1 * 2 + 2 * 2 = 8,从山顶返回到地面0需要消耗体力 2 * 1 + 1 * 1 + 1 * 1 = 4 的体力,按照登山路线 0 → 3 → 0 需要消耗体力12。攀登者至少需要12以上的体力(大于12)才能安全返回。
输入描述
第一行输入为地图一维数组
第二行输入为攀登者的体力,1,4,
输出描述
确保可以安全返回地面,且无生命危险的情况下,地图中有多少山峰可以攀登。
示例:
| 输入 | 0,1,4,3,1,0,0,1,2,3,1,2,1,0 13 |
|---|---|
| 输出 | 3 |
| 说明 | 登山者只能登上位置10和12的山峰,7 → 10 → 7,14 → 12 → 14 |
题目解析
本题考试时为核心代码模式,非ACM模式,即无需自己解析输入数据。
ython算法源码
class MountainClimbing:
def __init__(self, heights):
self.heights = heights
def climb_peaks(self, power_max):
ans = set()
space_list = []
n = len(self.heights)
i = 0
while i < n - 1:
if self.heights[i] == 0 and self.heights[i + 1] > 0:
space_list.append(i)
i += 1
for start in space_list:
i = start + 1
route_num = 0
while i < n and self.heights[i] != 0:
route_num += abs(self.heights[i] - self.heights[i - 1])
if route_num * 3 >= power_max:
break
if i == n - 1 and self.heights[i] > self.heights[i - 1]:
ans.add(i)
elif self.heights[i] > self.heights[i - 1] and self.heights[i] > self.heights[i + 1]:
ans.add(i)
i += 1
return len(ans)
# 输入高度数组
heights = list(map(int, input().split(",")))
# 获得数组长度
n = len(heights)
# 输入最大体力
power_max = int(input())
# 创建山峰攀登实例
climber = MountainClimbing(heights)
# 计算从左边空地出发攀爬的山峰数量
ans_from_left = climber.climb_peaks(power_max)
# 计算从右边空地出发攀爬的山峰数量
ans_from_right = climber.climb_peaks(power_max)
# 求两者的和作为总数
total_peaks = ans_from_left + ans_from_right
print(total_peaks),C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100000
// 全局变量,记录每个位置是否可以攀登
int canClimb[MAX_SIZE] = {0};
// 记录可以攀登的总数
int canClimb_count = 0;
// 定义一个结构体表示山
struct Mountain {
int *heights; // 山的高度数组
int size; // 山的高度数组大小
};
// 函数声明
void climbMountains(const int heights[], int size, int strength, int direction);
void reverseArray(int nums[], int size);
int findTotalPeaks(int heights[], int size, int strength);
// 主函数
int main() {
int heights[MAX_SIZE];
int size = 0;
// 输入山的高度数组
while (scanf("%d", &heights[size++])) {
if (getchar() != ',') break;
}
int strength;
scanf("%d", &strength);
// 输出结果
printf("%d\n", findTotalPeaks(heights, size, strength));
return 0;
}
// 函数:攀登山峰
void climbMountains(const int heights[], int size, int strength, int direction) {
int j = 0;
// 找到第一个地面位置
while (j < size && heights[j] != 0) {
j++;
}
int cost = 0;
// 开始攀登
for (int i = j + 1; i < size; i++) {
// 如果遇到了新的地面,则从新的地面位置重新计算攀登消耗的体力
if (heights[i] == 0) {
cost = 0;
continue;
}
// 计算当前位置与上一个位置的高度差
int diff = heights[i] - heights[i - 1];
if (diff > 0) {
// 如果是上坡
cost += diff * 3;
// 判断是否到达山顶
if (i + 1 >= size || heights[i] > heights[i + 1]) {
// 判断攀登消耗的体力是否小于等于当前体力值
if (cost < strength) {
// 根据攀登方向确定山峰位置
int idx = direction ? i : size - i - 1;
// 如果该位置可以攀登且未被标记过,则标记并增加可攀登总数
if (!canClimb[idx]) {
canClimb[i] = 1;
canClimb_count++;
}
}
}
} else if (diff < 0) {
// 如果是下坡
cost -= diff * 3;
}
}
}
// 函数:反转数组
void reverseArray(int nums[], int size) {
int i = 0;
int j = size - 1;
// 交换数组元素直到中间位置
while (i < j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
i++;
j--;
}
}
// 函数:计算可以攀登的山峰总数
int findTotalPeaks(int heights[], int size, int strength) {
// 正向攀登
climbMountains(heights, size, strength, 1);
// 反转数组后再次攀登
reverseArray(heights, size);
climbMountains(heights, size, strength, 0);
return canClimb_count;
}Java算法源码
import java.util.*;
// Point 代表坐标点
class Point {
int x;
int y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
public class Main {
// calcPeakCount,计算从指定起点出发能够攀登并按照原路返回的山峰数量
public static int calcPeakCount(List<Integer> heights, int startX, int powerMax, int n) {
int peakCount = 0;
int routeNum = 0;
int i = startX + 1;
while (i < n && heights.get(i) != 0) {
routeNum += Math.abs(heights.get(i) - heights.get(i - 1));
if (routeNum * 3 >= powerMax) {
break;
}
if ((i == n - 1 && heights.get(i) > heights.get(i - 1)) ||
(i < n - 1 && heights.get(i) > heights.get(i - 1) && heights.get(i) > heights.get(i + 1))) {
peakCount++;
}
i++;
}
return peakCount;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String input = scanner.nextLine();
List<Integer> heights = new ArrayList<>();
String[] heightStrings = input.split(",");
for (String heightString : heightStrings) {
heights.add(Integer.parseInt(heightString));
}
int n = heights.size();
int powerMax = scanner.nextInt();
// 使用 LinkedList 存储起始空地的坐标点
LinkedList<Point> startPoints = new LinkedList<>();
// 找出起始空地的坐标点
for (int i = 0; i < n - 1; i++) {
if (heights.get(i) == 0 && heights.get(i + 1) > 0) {
startPoints.add(new Point(i, heights.get(i)));
}
}
// 使用 HashSet 存储结果,确保结果的唯一性
HashSet<Integer> ansSet = new HashSet<>();
// 遍历每个起始空地点
for (Point startPoint : startPoints) {
int startX = startPoint.x;
int peakCount = calcPeakCount(heights, startX, powerMax, n);
ansSet.add(peakCount);
}
// 输出结果
System.out.println(ansSet.size());
}
}
3 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]