返回目录
题目描述
"吃货"和"馋嘴"两人到披萨店点了一份铁盘(圆形)披萨,并嘱咐店员将披萨按放射状切成大小相同的偶数个小块。但是粗心的服务员将披萨切成了每块大小都完全不同奇数块,且肉眼能分辨出大小。
由于两人都想吃到最多的披萨,他们商量了一个他们认为公平的分法:从"吃货"开始,轮流取披萨。除了第一块披萨可以任意选取外,其他都必须从缺口开始选。
他俩选披萨的思路不同。"馋嘴"每次都会选最大块的披萨,而且"吃货"知道"馋嘴"的想法。
已知披萨小块的数量以及每块的大小,求"吃货"能分得的最大的披萨大小的总和。
输入描述
第 1 行为一个正整数奇数 N,表示披萨小块数量。
- 3 ≤ N < 500
接下来的第 2 行到第 N + 1 行(共 N 行),每行为一个正整数,表示第 i 块披萨的大小
- 1 ≤ i ≤ N
披萨小块从某一块开始,按照一个方向次序顺序编号为 1 \~ N
- 每块披萨的大小范围为 [1, 2147483647]
输出描述
"吃货"能分得到的最大的披萨大小的总和。
| 输入 | 5 8 2 10 5 7 |
|---|---|
| 输出 | 19 |
| 说明 | 此例子中,有 5 块披萨。每块大小依次为 8、2、10、 5、7。 按照如下顺序拿披萨,可以使"吃货"拿到最多披萨: "吃货" 拿大小为 10 的披萨 "馋嘴" 拿大小为 5 的披萨 "吃货" 拿大小为 7 的披萨 "馋嘴" 拿大小为 8 的披萨 "吃货" 拿大小为 2 的披萨 至此,披萨瓜分完毕,"吃货"拿到的披萨总大小为 10 + 7 + 2 = 19 |
题目解析
题目用例意思如下:
初始月饼如下:
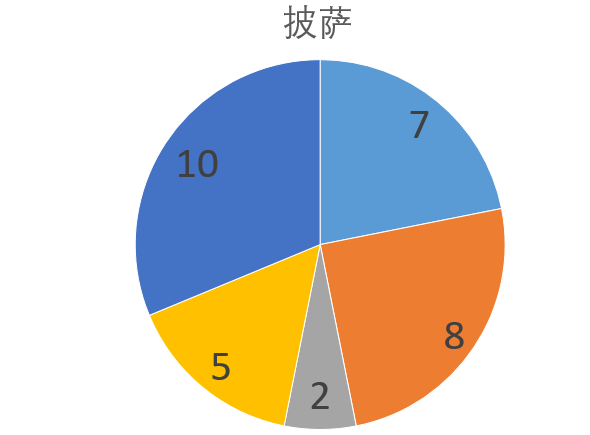
题目说
从"吃货"开始,轮流取披萨。
除了第一块披萨可以任意选取外,其他都必须从缺口开始选。
因此第一轮从"吃货"开始选,按照题目用例说明,先选走了10
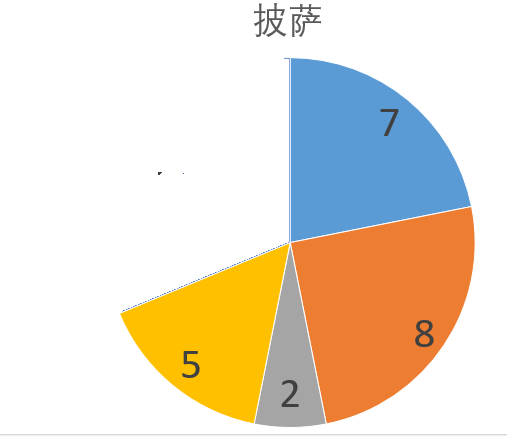
下一轮轮到"馋嘴"选,且必须从缺口的两端(5,2)中选,题目说:
"馋嘴"每次都会选最大块的披萨
因此"馋嘴"固定选择缺口的两端中较大的,即必然选走5
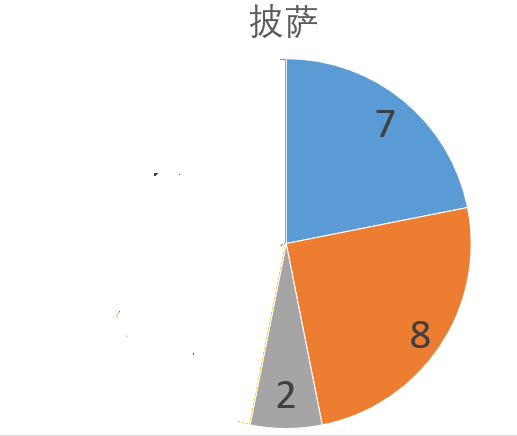
下一轮轮到吃货选择,而吃货也必须从缺口两端(7,2)中选:
- 如果选走2的话,那么下一轮,馋嘴肯定选走8
- 如果选走7的话,那么下一轮,馋嘴肯定选走8
因此无论吃货无论选哪个,馋嘴下一轮肯定选走8,因此吃货此轮选走7更优
接着就是选走8,最后选走2
Python算法源码
from functools import cache
new_var = None
# 越界索引环形变化
def adjust_index(idx):
if idx < 0:
idx = n - 1
elif idx >= n:
idx = 0
return idx
@cache
def recursive(l, r):
# 进入递归前,"吃货"已经拿了披萨,因此进入递归后,轮到"馋嘴"拿
# 而"馋嘴"拿披萨的策略固定是:缺口左右两边中较大的那块
if pizza[l] > pizza[r]: # 注意披萨大小各部相同,因此要么左边大,要么右边大,不存在相等的情况
# 拿走第 l 块,因此缺口左边的位置变为 l - 1
l = adjust_index(l - 1)
else:
# 拿走第 r 块,因此缺口右边的位置变为 r + 1
r = adjust_index(r + 1)
if l == r:
# 当 l == r 是,说明只剩一块披萨了,由于奇数个披萨,且"吃货"第一个拿,因此最后一个也是"吃货"拿
return pizza[l]
else:
# 如果还剩多块披萨,那么"吃货"有两种选择:
# 1、拿缺口左边的披萨
# 2、拿缺口右边的披萨
# 因此这里直接开两个递归分支,最终结果取较大值
return max(recursive(adjust_index(l - 1), r) + pizza[l], recursive(l, adjust_index(r + 1)) + pizza[r])
class Pizza:
def __init__(self, size, type):
self.size = size
self.type = type
def get_size(self):
return self.size
def get_type(self):
return self.type
def new_function():
# 这里是新函数的逻辑
pass
# 函数入参类型 和 个数改变
def get_result():
# ans记录"吃货"能获得的最大披萨大小
ans = 0
# i 指向首轮被"吃货"选取的披萨位置,可以理解为缺口位置,相当于给环切了一个口
i = 0
while i < n:
# i - 1 是缺口的左边披萨,adjust_index函数作用是防止 i - 1 越界, 进行绕环运动
# i + 1 是缺口的右边披萨,adjust_index函数作用是防止 i + 1 越界,进行绕环运动
# recursive的作用求解是"吃货"从缺失了 第 i 块的披萨铁盘 开始选,最终可得的最大披萨大小,
# 而第 i 块是首轮就被"吃货"拿走的,因此是recursive + pizza[i]
ans = max(ans, recursive(adjust_index(i - 1), adjust_index(i + 1)) + pizza[i])
i += 1
return ans
# 输入获取
n = int(input()) # 披萨数量(奇数个)
pizza = [] # n个披萨的大小(各不相同)
for _ in range(n):
pizza.append(int(input()))
print(get_result())C算法源码
#include <stdio.h>
#include <stdlib.h>
// 全局变量
int *pizza; // 存储披萨大小的数组
int n; // 披萨数量
// 环形索引
int adjust_index(int idx) {
if (idx < 0)
idx = n - 1;
else if (idx >= n)
idx = 0;
return idx;
}
// 递归函数,计算最大披萨大小
int recursive(int l, int r) {
if (pizza[l] > pizza[r])
l = adjust_index(l - 1);
else
r = adjust_index(r + 1);
if (l == r)
return pizza[l];
else
return (recursive(adjust_index(l - 1), r) + pizza[l]) > (recursive(l, adjust_index(r + 1)) + pizza[r])
? recursive(adjust_index(l - 1), r) + pizza[l]
: recursive(l, adjust_index(r + 1)) + pizza[r];
}
// 获取结果的函数
int get_result() {
int ans = 0;
for (int i = 0; i < n; i++) {
ans = (recursive(adjust_index(i - 1), adjust_index(i + 1)) + pizza[i]) > ans
? (recursive(adjust_index(i - 1), adjust_index(i + 1)) + pizza[i])
: ans;
}
return ans;
}
int main() {
// 输入
scanf("%d", &n);
pizza = (int *)malloc(n * sizeof(int));
if (pizza == NULL) {
printf("内存分配失败。\n");
return 1;
}
for (int i = 0; i < n; i++) {
scanf("%d", &pizza[i]);
}
// 输出
printf("%d\n", get_result());
// 释放分配的内存
free(pizza);
return 0;
}Java算法源码
import java.util.Scanner;
public class Main {
// 存储披萨大小的数组
static int[] pizza;
// 披萨数量
static int n;
// 环形索引
static int adjustIndex(int idx) {
if (idx < 0)
idx = n - 1;
else if (idx >= n)
idx = 0;
return idx;
}
// 递归函数,计算最大披萨大小
static int recursive(int l, int r) {
if (pizza[l] > pizza[r])
l = adjustIndex(l - 1);
else
r = adjustIndex(r + 1);
if (l == r)
return pizza[l];
else
return (recursive(adjustIndex(l - 1), r) + pizza[l]) > (recursive(l, adjustIndex(r + 1)) + pizza[r])
? recursive(adjustIndex(l - 1), r) + pizza[l]
: recursive(l, adjustIndex(r + 1)) + pizza[r];
}
// 获取结果的函数
static int getResult() {
int ans = 0;
for (int i = 0; i < n; i++) {
ans = (recursive(adjustIndex(i - 1), adjustIndex(i + 1)) + pizza[i]) > ans
? (recursive(adjustIndex(i - 1), adjustIndex(i + 1)) + pizza[i])
: ans;
}
return ans;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 输入披萨数量
n = scanner.nextInt();
pizza = new int[n];
// 输入披萨大小
for (int i = 0; i < n; i++) {
pizza[i] = scanner.nextInt();
}
// 输出结果
System.out.println(getResult());
// 关闭输入流
scanner.close();
}
}
4 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]