返回目录
题目描述
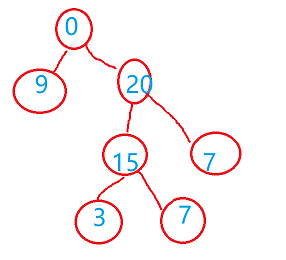
给定一个二叉树,每个节点上站一个人,节点数字表示父节点到该节点传递悄悄话需要花费的时间。
初始时,根节点所在位置的人有一个悄悄话想要传递给其他人,求二叉树所有节点上的人都接收到悄悄话花费的时间。
输入描述
给定二叉树
0 9 20 -1 -1 15 7 -1 -1 -1 -1 3 2
注:-1表示空节点
输出描述
返回所有节点都接收到悄悄话花费的时间
38
示例:
| 输入 | 0 9 20 -1 -1 15 7 -1 -1 -1 -1 3 2 |
|---|---|
| 输出 | 30 |
| 说明 | 无 |
Python算法源码
MAX_SIZE = 10000
class ListNode:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.size = 0
self.head = None
self.tail = None
def append(self, data):
"""向链表末尾添加新节点"""
new_node = ListNode(data)
if self.size == 0:
self.head = new_node
self.tail = new_node
else:
self.tail.next = new_node
self.tail = new_node
self.size += 1
def remove_first(self):
"""移除链表头部节点并返回其值"""
if self.size == 0:
exit(-1)
removed_node = self.head
if self.size == 1:
self.head = None
self.tail = None
else:
self.head = self.head.next
self.size -= 1
return removed_node.data
# 从标准输入中读取整数并存储到数组中
times = list(map(int, input().split()))
def getResult():
"""计算最大时延"""
# 记录题解
ans = 0
# 根节点的索引是0
queue = LinkedList()
queue.append(0)
while queue.size > 0:
fa = queue.remove_first() # 父节点索引
ch1 = 2 * fa + 1 # 左子节点索引
ch2 = 2 * fa + 2 # 右子节点索引
# fa是否存在左子节点
ch1_exist = ch1 < len(times) and times[ch1] != -1
# fa是否存在右子节点
ch2_exist = ch2 < len(times) and times[ch2] != -1
# fa如果存在左子节点
if ch1_exist:
times[ch1] += times[fa]
queue.append(ch1)
# fa如果存在右子节点
if ch2_exist:
times[ch2] += times[fa]
queue.append(ch2)
# fa是叶子节点
if not ch1_exist and not ch2_exist:
# 保留叶子节点中最大时延
ans = max(ans, times[fa])
return ans
# 算法调用
print(getResult())C算法源码
#include <stdio.h>
#include <stdlib.h>
#define MAX(x, y) ((x) > (y) ? (x) : (y))
#define MAX_SIZE 10000
typedef struct ListNode {
int data;
struct ListNode *next;
} ListNode;
typedef struct LinkedList {
int size;
ListNode *head;
ListNode *tail;
} LinkedList;
// 创建链表
LinkedList *createLinkedList() {
LinkedList *list = (LinkedList *) malloc(sizeof(LinkedList));
list->size = 0;
list->head = NULL;
list->tail = NULL;
return list;
}
// 在链表末尾添加节点
void appendLinkedList(LinkedList *list, int data) {
ListNode *newNode = (ListNode *) malloc(sizeof(ListNode));
newNode->data = data;
newNode->next = NULL;
if (list->size == 0) {
list->head = newNode;
list->tail = newNode;
} else {
list->tail->next = newNode;
list->tail = newNode;
}
list->size++;
}
// 移除链表的第一个节点
int removeFirstLinkedList(LinkedList* list) {
if (list->size == 0) exit(-1);
ListNode* removedNode = list->head;
if (list->size == 1) {
list->head = NULL;
list->tail = NULL;
} else {
list->head = list->head->next;
}
list->size--;
int result = removedNode->data;
free(removedNode);
return result;
}
int main() {
int values[MAX_SIZE];
int valuesSize = 0;
// 从标准输入中读取整数并存储到数组中
while (scanf("%d", &values[valuesSize++])) {
if (getchar() != ' ') break;
}
int maxDelay = 0;
LinkedList* queue = createLinkedList();
appendLinkedList(queue, 0);
// 遍历队列
while (queue->size > 0) {
int parentIndex = removeFirstLinkedList(queue); // 父节点索引
int leftChildIndex = 2 * parentIndex + 1; // 左子节点索引
int rightChildIndex = 2 * parentIndex + 2; // 右子节点索引
int leftChildExist = leftChildIndex < valuesSize && values[leftChildIndex] != -1; // 检查左子节点是否存在
int rightChildExist = rightChildIndex < valuesSize && values[rightChildIndex] != -1; // 检查右子节点是否存在
if (leftChildExist) {
values[leftChildIndex] += values[parentIndex];
appendLinkedList(queue, leftChildIndex);
}
if (rightChildExist) {
values[rightChildIndex] += values[parentIndex];
appendLinkedList(queue, rightChildIndex);
}
// 若左右子节点都不存在,则当前节点为叶子节点,更新最大延迟值
if (!leftChildExist && !rightChildExist) {
maxDelay = MAX(maxDelay, values[parentIndex]); // 保持叶子节点中的最大延迟值
}
}
printf("%d\n", maxDelay);
return 0;
}Java算法源码
import java.util.LinkedList;
import java.util.Scanner;
public class Main {
static class ListNode {
int ele;
ListNode next;
public ListNode(int ele) {
this.ele = ele;
this.next = null;
}
}
static class LinkedList {
int size;
ListNode head;
ListNode tail;
public LinkedList() {
this.size = 0;
this.head = null;
this.tail = null;
}
public void addLast(int ele) {
ListNode listNode = new ListNode(ele);
if (size == 0) {
head = listNode;
tail = listNode;
} else {
tail.next = listNode;
tail = listNode;
}
size++;
}
public int removeFirst() {
if (size == 0) throw new IllegalStateException();
ListNode removed = head;
if (size == 1) {
head = null;
tail = null;
} else {
head = head.next;
}
size--;
int res = removed.ele;
return res;
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int[] times = new int[10000];
int timesSize = 0;
// 读取输入,存储在数组中
while (scanner.hasNextInt()) {
times[timesSize++] = scanner.nextInt();
if (!scanner.hasNext()) break;
}
int ans = 0;
LinkedList queue = new LinkedList();
queue.addLast(0);
// 进行广度优先搜索
while (queue.size > 0) {
int fa = queue.removeFirst(); // 移除队列头部元素作为父节点
int ch1 = 2 * fa + 1; // 左子节点索引
int ch2 = 2 * fa + 2; // 右子节点索引
boolean ch1Exist = ch1 < timesSize && times[ch1] != -1; // 判断左子节点是否存在
boolean ch2Exist = ch2 < timesSize && times[ch2] != -1; // 判断右子节点是否存在
// 如果左子节点存在,则更新左子节点的时间,并将其加入队列
if (ch1Exist) {
times[ch1] += times[fa];
queue.addLast(ch1);
}
// 如果右子节点存在,则更新右子节点的时间,并将其加入队列
if (ch2Exist) {
times[ch2] += times[fa];
queue.addLast(ch2);
}
// 如果当前节点为叶子节点,则更新答案
if (!ch1Exist && !ch2Exist) {
ans = Math.max(ans, times[fa]);
}
}
// 输出结果
System.out.println(ans);
}
}
5 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]真题目录序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指针☆☆☆☆13掌[...]