返回目录

题目描述：

定义构造三叉搜索树规则如下：

每个节点都存有一个数，当插入一个新的数时，从根节点向下寻找，直到找到一个合适的空节点插入。
查找的规则是：

1. 如果数小于节点的数减去500，则将数插入节点的左子树
2. 如果数大于节点的数加上500，则将数插入节点的右子树
3. 否则，将数插入节点的中子树
   给你一系列数，请按以上规则，按顺序将数插入树中，构建出一棵三叉搜索树，最后输出树的高度。

输入描述：

第一行为一个数N，表示有N个数，1<=N<=10000
第二行为N个空格分隔的整数，每个数的范围为[1,10000]

输出描述：

输出树的高度(根节点的高度为1)

示例：

输入	3 5000 4000 3000
输出	3
说  明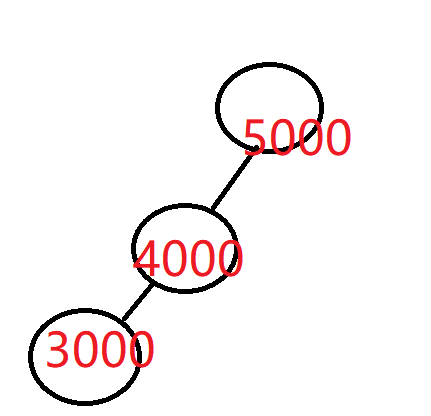

题目解析

本题应该只是需要模拟出三叉树结构，以及根据指定的逻辑进行插入新节点。

三叉树节点的数据结构定义如下：

{
val， // 节点值
height，// 节点所在高度，
left，// 左子树根节点，
right，// 右子树根节点，
mid，// 中子树根节点
}

三叉树的数据结构定义如下：

{
root，// 根节点
height，// 树的高度
}

Python算法源码

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.height = -1  # 初始化高度为 -1，表示未分配的节点
        self.left = None
        self.mid = None
        self.right = None

class Tree:
    def __init__(self):
        self.root = None  # 根节点
        self.height = 0  # 树的高度

    # 添加节点到树中
    def add(self, val):
        node = TreeNode(val)  # 创建新节点

        # 如果根节点为空，则将新节点设为根节点
        if self.root is None:
            node.height = 1  # 新节点高度设为 1
            self.root = node
            self.height = 1  # 树高度设为 1
        else:
            cur = self.root

            # 遍历树找到合适的位置插入新节点
            while True:
                node.height = cur.height + 1  # 更新新节点高度
                self.height = max(node.height, self.height)  # 更新树的高度

                # 如果新节点值比当前节点值小 500 以上，则插入当前节点的左子树
                if val < cur.val - 500:
                    # 如果当前节点的左子节点为空，则将新节点设为左子节点，否则继续向左子树遍历
                    if cur.left is None:
                        cur.left = node
                        break
                    else:
                        cur = cur.left
                # 如果新节点值比当前节点值大 500 以上，则插入当前节点的右子树
                elif val > cur.val + 500:
                    # 如果当前节点的右子节点为空，则将新节点设为右子节点，否则继续向右子树遍历
                    if cur.right is None:
                        cur.right = node
                        break
                    else:
                        cur = cur.right
                # 否则插入当前节点的中间子树
                else:
                    # 如果当前节点的中间子节点为空，则将新节点设为中间子节点，否则继续向中间子树遍历
                    if cur.mid is None:
                        cur.mid = node
                        break
                    else:
                        cur = cur.mid

if __name__ == "__main__":
    while True:
        try:
            n = int(input())  # 读取整数 n
            nums = list(map(int, input().split()))  # 读取一

C算法源码

#include <stdio.h>
#include <stdlib.h>

// 定义树节点结构体
typedef struct TreeNode {
    int val; // 节点值
    int height; // 节点高度
    struct TreeNode *left, *mid, *right; // 左、中、右子节点
} TreeNode;

// 定义树结构体
typedef struct Tree {
    TreeNode *root; // 根节点
    int height; // 树的高度
} Tree;

// 创建树节点
TreeNode* createTreeNode(int val) {
    TreeNode *node = (TreeNode*)malloc(sizeof(TreeNode)); // 分配内存空间
    if (node != NULL) {
        node->val = val;
        node->height = -1; // 初始化高度为 -1，表示未分配的节点
        node->left = node->mid = node->right = NULL; // 初始化子节点为 NULL
    }
    return node;
}

// 初始化树
Tree* createTree() {
    Tree *tree = (Tree*)malloc(sizeof(Tree)); // 分配内存空间
    if (tree != NULL) {
        tree->root = NULL;
        tree->height = 0;
    }
    return tree;
}

// 添加节点到树中
void addNode(Tree *tree, int val) {
    TreeNode *node = createTreeNode(val); // 创建新节点

    // 如果根节点为空，则将新节点设为根节点
    if (tree->root == NULL) {
        node->height = 1; // 新节点高度设为 1
        tree->root = node;
        tree->height = 1; // 树高度设为 1
    } else {
        TreeNode *cur = tree->root;

        // 遍历树找到合适的位置插入新节点
        while (1) {
            node->height = cur->height + 1; // 更新新节点高度
            tree->height = (node->height > tree->height) ? node->height : tree->height; // 更新树的高度

            // 如果新节点值比当前节点值小 500 以上，则插入当前节点的左子树
            if (val < cur->val - 500) {
                // 如果当前节点的左子节点为空，则将新节点设为左子节点，否则继续向左子树遍历
                if (cur->left == NULL) {
                    cur->left = node;
                    break;
                } else {
                    cur = cur->left;
                }
            } 
            // 如果新节点值比当前节点值大 500 以上，则插入当前节点的右子树
            else if (val > cur->val + 500) {
                // 如果当前节点的右子节点为空，则将新节点设为右子节点，否则继续向右子树遍历
                if (cur->right == NULL) {
                    cur->right = node;
                    break;
                } else {
                    cur = cur->right;
                }
            } 
            // 否则插入当前节点的中间子树
            else {
                // 如果当前节点的中间子节点为空，则将新节点设为中间子节点，否则继续向中间子树遍历
                if (cur->mid == NULL) {
                    cur->mid = node;
                    break;
                } else {
                    cur = cur->mid;
                }
            }
        }
    }
}

int main() {
    while (1) {
        int n;
        if (scanf("%d", &n) != 1)
            break;

        int val;
        Tree *tree = createTree(); // 创建树对象

        // 将整数值添加到树中
        for (int i = 0; i < n; i++) {
            scanf("%d", &val);
            addNode(tree, val);
        }

        printf("%d\n", tree->height); // 输出树的高度
    }

    return 0;
}

Java算法源码

import java.util.Scanner;

// 定义树节点类
class TreeNode {
    int val; // 节点值
    int height; // 节点高度
    TreeNode left, mid, right; // 左、中、右子节点

    // 构造函数，初始化节点值和高度，子节点初始化为 null
    public TreeNode(int val) {
        this.val = val;
        this.height = -1; // 初始化高度为 -1，表示未分配的节点
        this.left = this.mid = this.right = null;
    }
}

// 定义树类
class Tree {
    TreeNode root; // 根节点
    int height; // 树的高度

    // 构造函数，初始化根节点为 null，高度为 0
    public Tree() {
        this.root = null;
        this.height = 0;
    }

    // 添加节点到树中
    public void add(int val) {
        TreeNode node = new TreeNode(val); // 创建新节点

        // 如果根节点为空，则将新节点设为根节点
        if (root == null) {
            node.height = 1; // 新节点高度设为 1
            root = node;
            height = 1; // 树高度设为 1
        } else {
            TreeNode cur = root;

            // 遍历树找到合适的位置插入新节点
            while (true) {
                node.height = cur.height + 1; // 更新新节点高度
                height = Math.max(node.height, height); // 更新树的高度

                // 如果新节点值比当前节点值小 500 以上，则插入当前节点的左子树
                if (val < cur.val - 500) {
                    // 如果当前节点的左子节点为空，则将新节点设为左子节点，否则继续向左子树遍历
                    if (cur.left == null) {
                        cur.left = node;
                        break;
                    } else {
                        cur = cur.left;
                    }
                } 
                // 如果新节点值比当前节点值大 500 以上，则插入当前节点的右子树
                else if (val > cur.val + 500) {
                    // 如果当前节点的右子节点为空，则将新节点设为右子节点，否则继续向右子树遍历
                    if (cur.right == null) {
                        cur.right = node;
                        break;
                    } else {
                        cur = cur.right;
                    }
                } 
                // 否则插入当前节点的中间子树
                else {
                    // 如果当前节点的中间子节点为空，则将新节点设为中间子节点，否则继续向中间子树遍历
                    if (cur.mid == null) {
                        cur.mid = node;
                        break;
                    } else {
                        cur = cur.mid;
                    }
                }
            }
        }
    }
}

// 主类
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        // 无限循环，直到捕获到异常结束程序
        while (true) {
            try {
                int n = Integer.parseInt(scanner.nextLine()); // 读取整数 n
                String[] nums = scanner.nextLine().split(" "); // 读取一系列整数值并以空格分隔

                Tree tree = new Tree(); // 创建树对象
                // 将整数值添加到树中
                for (String num : nums) {
                    tree.add(Integer.parseInt(num));
                }

                System.out.println(tree.height); // 输出树的高度
            } catch (Exception e) {
                break; // 捕获异常时结束循环
            }
        }
    }
}