返回目录
题目描述
从前有个村庄,村民们喜欢在各种田地上插上小旗子,旗子上标识了各种不同的数字。
某天集体村民决定将覆盖相同数字的最小矩阵形的土地分配给村里做出巨大贡献的村民,请问此次分配土地,做出贡献的村民种最大会分配多大面积?
输入描述
第一行输入 m 和 n,
- m 代表村子的土地的长
- n 代表土地的宽
第二行开始输入地图上的具体标识
输出描述
此次分配土地,做出贡献的村民种最大会分配多大面积
示例:
| 输入 | 33 101 000 010 |
|---|---|
| 输出 | 9 |
| 说明 | 土地上的旗子为1,其坐标分别 为(0,0),(2,1)以及(0,2),为了 覆盖所有旗子,矩阵需要覆盖 的横坐标为0和2,纵坐标为0和 2,所以面积为9, 即(2-0+1)*(2-0+1)= 9 |
| 输入 | 33 102 000 034 |
|---|---|
| 输出 | 1 |
| 说明 | 由于不存在成对的小旗子, 故而返回1,即一块土地的面积。 |
题目解析
根据用例1说明来看,最小矩形需要覆盖相同数字得所有旗子。
土地上的旗子为1,其坐标分别为(0,0),(2,1)以及(0,2),为了覆盖所有旗子,矩阵需要覆盖的横坐标为0和2,纵坐标为0和2,所以面积为9,即(2-0+1)*(2-0+1)= 9
但是这产生一个问题?比如下图所示:
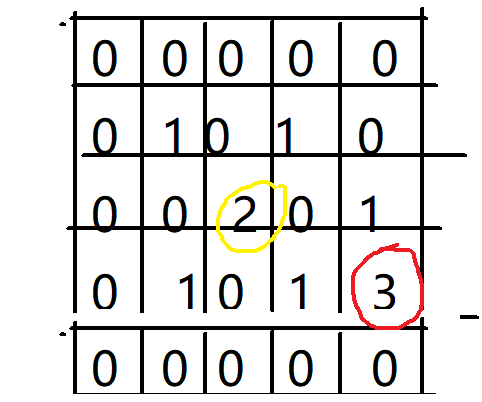
如果我要覆盖住所有的数字1,那么必然会同时覆盖了数字2,3,此时该怎么办呢?
题目没有说怎么处理,那么我理解就不需要管,只需要保证覆盖所有1的矩形最小就行。
本题解题思路很简单,只需要统计出相同数字的出现的“所有坐标位置”中:
- 最小的横坐标(矩形最上面一行的行号)
- 最大的横坐标(矩形最下面一行的行号)
- 最小的纵坐标(矩形最左边一列的列号)
- 最大的纵坐标(矩形最右边一列的列号)
即可。比如:前面图示中数字1的所有坐标位置(1,1)、(1,3)、(2,4)、(3,1)、(3,3)中:
- 最小的横坐标:1
- 最大的横坐标:3
- 最小的纵坐标:1
- 最大的纵坐标:4
那么包含所有数字1的最小矩形面积为:
(最大的横坐标 - 最小的横坐标 + 1) * (最大的纵坐标 - 最小的纵坐标 + 1)
Python算法源码
import sys
additional_variable = 0
class Rect:
def __init__(self):
self.minRow = sys.maxsize
self.maxRow = -sys.maxsize
self.minCol = sys.maxsize
self.maxCol = -sys.maxsize
def setRowCol(self, val, rowCol):
if rowCol == 0:
self.minRow = min(self.minRow, val)
self.maxRow = max(self.maxRow, val)
else:
self.minCol = min(self.minCol, val)
self.maxCol = max(self.maxCol, val)
def printRectInfo(rect):
print(f"Rect Info: minRow={rect.minRow}, maxRow={rect.maxRow}, minCol={rect.minCol}, maxCol={rect.maxCol}")
# 输入获取
m, n = map(int, input().split())
rects = {}
i = 0
while i < m:
nums = list(map(int, input().split()))
j = 0
while j < n:
num = nums[j]
if num > 0:
if num not in rects:
rects[num] = Rect()
rects[num].setRowCol(i, 0)
rects[num].setRowCol(j, 1)
j += 1
i += 1
maxArea = 0
for num in rects:
rect = rects[num]
maxArea = max(maxArea, (rect.maxRow - rect.minRow + 1) * (rect.maxCol - rect.minCol + 1))
print(maxArea)C算法源码
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
int additional_variable = 0;
#define MIN_VAL(x, y) ((x) < (y) ? (x) : (y))
#define MAX_VAL(x, y) ((x) > (y) ? (x) : (y))
#define MAX_RECTS 500
typedef struct {
int minRow;
int maxRow;
int minCol;
int maxCol;
} Rect;
Rect *createRect() {
Rect *rect = (Rect *)malloc(sizeof(Rect));
rect->minRow = INT_MAX;
rect->maxRow = INT_MIN;
rect->minCol = INT_MAX;
rect->maxCol = INT_MIN;
return rect;
}
void setRowCol(Rect *rect, int val, int rowCol) {
if (rowCol == 0) {
rect->minRow = MIN_VAL(rect->minRow, val);
rect->maxRow = MAX_VAL(rect->maxRow, val);
} else {
rect->minCol = MIN_VAL(rect->minCol, val);
rect->maxCol = MAX_VAL(rect->maxCol, val);
}
}
void printRectInfo(Rect *rect) {
printf("Rect Info: minRow=%d, maxRow=%d, minCol=%d, maxCol=%d\n",
rect->minRow, rect->maxRow, rect->minCol, rect->maxCol);
}
int main() {
int rows, cols;
scanf("%d %d", &rows, &cols);
Rect *rects[MAX_RECTS] = {NULL};
int i = 0;
while (i < rows) {
int j = 0;
while (j < cols) {
int num;
scanf("%d", &num);
if (num > 0) {
if (rects[num] == NULL) {
rects[num] = createRect();
}
setRowCol(rects[num], i, 0);
setRowCol(rects[num], j, 1);
}
j++;
}
i++;
}
int maxArea = 0;
for (int i = 0; i < MAX_RECTS; i++) {
Rect *rect = rects[i];
if (rect != NULL) {
int area = (rect->maxRow - rect->minRow + 1) * (rect->maxCol - rect->minCol + 1);
maxArea = MAX_VAL(maxArea, area);
}
}
printf("%d\n", maxArea);
return 0;
}Java算法源码
import java.util.HashMap;
import java.util.Scanner;
public class Main {
static int additionalVariable = 0;
static class Rectangle {
int minRow = Integer.MAX_VALUE;
int maxRow = Integer.MIN_VALUE;
int minCol = Integer.MAX_VALUE;
int maxCol = Integer.MIN_VALUE;
private void setRowCol(int val, int rowCol) {
if (rowCol == 0) {
this.minRow = Math.min(this.minRow, val);
this.maxRow = Math.max(this.maxRow, val);
} else {
this.minCol = Math.min(this.minCol, val);
this.maxCol = Math.max(this.maxCol, val);
}
}
}
static void printRectangleInfo(Rectangle rectangle) {
System.out.println("Rect Info: minRow=" + rectangle.minRow + ", maxRow=" + rectangle.maxRow +
", minCol=" + rectangle.minCol + ", maxCol=" + rectangle.maxCol);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int rows = scanner.nextInt(); // 长(行数)
int cols = scanner.nextInt(); // 宽(列数)
HashMap<Integer, Rectangle> rectangles = new HashMap<>();
int i = 0;
while (i < rows) {
int j = 0;
while (j < cols) {
int num = scanner.nextInt();
if (num > 0) {
rectangles.putIfAbsent(num, new Rectangle());
rectangles.get(num).setRowCol(i, 0);
rectangles.get(num).setRowCol(j, 1);
}
j++;
}
i++;
}
int maxArea = 0;
for (int num : rectangles.keySet()) {
Rectangle rectangle = rectangles.get(num);
maxArea = Math.max(maxArea, (rectangle.maxRow - rectangle.minRow + 1) * (rectangle.maxCol - rectangle.minCol + 1));
}
System.out.println(maxArea);
}
}
6 条评论
def main():
# m ,n 表示长和宽
m, n = map(int, input().split())
i = 0
x_min = 0
x_max = 0
y_min = 0
y_max = 0
while i < m:
my_list = list(map(int, input().split()))
for index in range(len(my_list)):
if my_list[index] == 1:
if index > y_max:
y_max = index
if index < y_min:
y_min = index
if i < x_min:
x_min = i
if i > x_max:
x_max = i
i = i + 1
print((x_max - x_min + 1) * (y_max - y_min + 1))
if __name__ == '__main__':
main()
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]真题目录序号题目 1密码输入检测 2分配土地 3找座位 4智能成绩表 5内存冷热标记 6螺旋数字矩阵 机器人搬砖 转盘寿司 提取字符串的最长合法简单数学表达式 2最富裕的小家庭 3最长字符串的长度(一) 开源项目热度榜单 游戏分组 虚拟理财游戏[...]