返回目录
题目描述
下图中,每个方块代表一个像素,每个像素用其行号和列号表示。为简化处理,多段线的走向只能是水平、竖直、斜向45度。
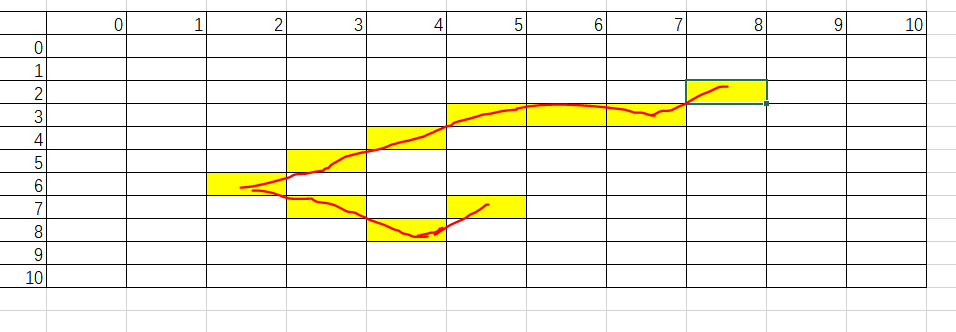
上图中的多段线可以用下面的坐标串表示:(2, 8), (3, 7), (3, 6), (3, 5), (4, 4), (5, 3), (6, 2), (7, 3), (8, 4), (7, 5)。
但可以发现,这种表示不是最简的,其实只需要存储6个蓝色的关键点即可,它们是线段的起点、拐点、终点,而剩下4个点是冗余的。
即可以简化为:(2,8)、(3,7)、(3,5)、(6,2)、(8,4)、(7,5)
现在,请根据输入的包含有冗余数据的多段线坐标列表,输出其最简化的结果。
输入描述
2 8 3 7 3 6 3 5 4 4 5 3 6 2 7 3 8 4 7 5
1、所有数字以空格分隔,每两个数字一组,第一个数字是行号,第二个数字是列号;
2、行号和列号范围为[0,64),用例输入保证不会越界,考生不必检查;
3、输入数据至少包含两个坐标点。
输出描述
2 8 3 7 3 5 6 2 8 4 7 5
压缩后的最简化坐标列表,和输入数据的格式相同。
备注: 输出的坐标相对顺序不能变化。
示例:
| 输入 | 2 8 3 7 3 6 3 5 4 4 5 3 6 2 7 3 8 4 7 5 |
|---|---|
| 输出 | 2 8 3 7 3 5 6 2 8 4 7 5 |
| 说明 | 如上图所示,6个蓝色像素的坐标依次是(2,8)、(3,7)、(3,5)、(6,2)、(8,4)、(7,5)。 |
解题思路
遍历输入的坐标点列表,对于每个当前考察的点 curr,检查它是否是拐点。为此,比较它与前一个点 prev 以及后一个点 next 形成的两个向量。如果这两个向量不共线(即它们的叉积不为零),则当前点是一个拐点。
向量和向量的叉积(cross product)。
- 向量:在二维平面中,向量可以用来表示两点之间的方向和距离。在这段代码中,向量是由两个点确定的,例如,向量
(dx1, dy1)是由点prev指向点curr的向量,而向量(dx2, dy2)是由点curr指向点next的向量。 - 向量的叉积:在二维空间中,两个向量
a(x1, y1)和b(x2, y2)的叉积定义为a.x * b.y - a.y * b.x,即x1 * y2 - y1 * x2。叉积的结果是一个标量,它的绝对值等于以这两个向量为边的平行四边形的面积。叉积的符号表示这两个向量的相对方向,如果叉积为正,则b向量在a向量的逆时针方向;如果叉积为负,则b向量在a向量的顺时针方向;如果叉积为零,则两个向量共线。
下面的代码中,叉积用于判断三个连续的点 prev、curr、next 是否构成一个拐点。如果 prev 到 curr 的向量 (dx1, dy1) 与 curr 到 next 的向量 (dx2, dy2) 的叉积不为零,即 dx1 * dy2 != dy1 * dx2,则说明这两个向量不共线,即 curr 点是一个拐点。如果叉积为零,则表示这三个点共线,curr 点不是拐点。
Python算法源码
import sys
def readline():
return sys.stdin.readline().strip()
def get_result(nums):
ans = []
# 上一个点坐标(preX, preY)
preX, preY = nums[0], nums[1]
# 上一次的运动方向(preDirectX, preDirectY)
preDirectX, preDirectY = 0, 0
for i in range(2, len(nums), 2):
# 当前点坐标(curX, curY)
curX, curY = nums[i], nums[i + 1]
# 上一个点到当前点的偏移量(offsetX, offsetY)
offsetX, offsetY = curX - preX, curY - preY
# 根据偏移量得出本次的运动方向
base = max(abs(offsetX), abs(offsetY))
directX, directY = offsetX / base, offsetY / base
# 如果两次运动的方向不同
if directX != preDirectX or directY != preDirectY:
# 则上一个点是拐点,需要记录下来
ans.extend([str(preX), str(preY)])
preX, preY = curX, curY
preDirectX, preDirectY = directX, directY
# 注意收尾
ans.extend([str(preX), str(preY)])
return " ".join(ans)
if __name__ == "__main__":
nums = list(map(int, input().split()))
print(get_result(nums))C算法源码
#include <stdio.h>
#include <stdlib.h>
int main() {
// 读取输入点
int x, y;
int preX, preY, preDirectX, preDirectY;
int offsetX, offsetY, base;
int numPoints = 0;
int maxPoints = 1000; // 假设最多1000个点
int **points = (int **)malloc(maxPoints * sizeof(int *));
if (points == NULL) {
fprintf(stderr, "内存分配失败\n");
exit(1);
}
while (scanf("%d %d", &x, &y) == 2) {
points[numPoints] = (int *)malloc(2 * sizeof(int));
if (points[numPoints] == NULL) {
fprintf(stderr, "内存分配失败\n");
exit(1);
}
points[numPoints][0] = x;
points[numPoints][1] = y;
numPoints++;
}
// 上一个点坐标(preX, preY)
preX = points[0][0];
preY = points[0][1];
// 上一次的运动方向(preDirectX, preDirectY)
preDirectX = 0;
preDirectY = 0;
// 输出简化后的路径
printf("%d %d ", preX, preY);
for (int i = 1; i < numPoints; i++) {
// 当前点坐标(curX, curY)
int curX = points[i][0];
int curY = points[i][1];
// 上一个点到当前点的偏移量(offsetX, offsetY)
offsetX = curX - preX;
offsetY = curY - preY;
// 根据偏移量得出本次的运动方向
base = abs(offsetX) > abs(offsetY) ? abs(offsetX) : abs(offsetY);
double directX = (double)offsetX / base;
double directY = (double)offsetY / base;
// 如果两次运动的方向不同
if (directX != preDirectX || directY != preDirectY) {
// 则上一个点是拐点,需要记录下来
printf("%d %d ", preX, preY);
}
preX = curX;
preY = curY;
preDirectX = directX;
preDirectY = directY;
}
// 注意收尾
printf("%d %d\n", preX, preY);
// 释放动态分配的内存
for (int i = 0; i < numPoints; i++) {
free(points[i]);
}
free(points);
return 0;
}Java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String[] input = scanner.nextLine().split(" ");
int[] nums = new int[input.length];
for (int i = 0; i < input.length; i++) {
nums[i] = Integer.parseInt(input[i]);
}
System.out.println(getResult(nums));
}
public static String getResult(int[] nums) {
StringBuilder sb = new StringBuilder();
// 上一个点坐标(preX, preY)
int preX = nums[0];
int preY = nums[1];
// 上一次的运动方向(preDirectX, preDirectY)
int preDirectX = 0;
int preDirectY = 0;
for (int i = 2; i < nums.length; i += 2) {
// 当前点坐标(curX, curY)
int curX = nums[i];
int curY = nums[i + 1];
// 上一个点到当前点的偏移量(offsetX, offsetY)
int offsetX = curX - preX;
int offsetY = curY - preY;
// 根据偏移量得出本次的运动方向
int base = Math.max(Math.abs(offsetX), Math.abs(offsetY));
int directX = offsetX / base;
int directY = offsetY / base;
// 如果两次运动的方向不同
if (directX != preDirectX || directY != preDirectY) {
// 则上一个点是拐点,需要记录下来
sb.append(preX).append(" ").append(preY).append(" ");
}
preX = curX;
preY = curY;
preDirectX = directX;
preDirectY = directY;
}
// 注意收尾
sb.append(preX).append(" ").append(preY);
return sb.toString();
}
}
3 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]