题目描述

给定长度为 n nn 的无序的数字数组，每个数字代表二叉树的叶子节点的权值，数字数组的值均大于等于 1 11 。请完成一个函数，根据输入的数字数组，生成哈夫曼树，并将哈夫曼树按照中序遍历输出。
为了保证输出的二叉树中序遍历结果统一，增加以下限制:又树节点中，左节点权值小于等于右节点权值，根节点权值为左右节点权值之和。当左右节点权值相同时，左子树高度高度小于等于右子树。
注意:所有用例保证有效，并能生成哈夫曼树提醒:哈夫曼树又称最优二叉树，是一种带权路径长度最短的一叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为 0 00 层，叶结点到根结点的路径长度为叶结点的层数)

输入描述

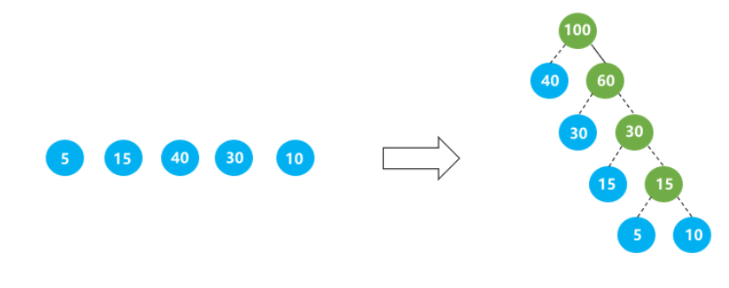
例如：由叶子节点 5 15 40 30 10 生成的最优二叉树如下图所示，该树的最短带权路径长度为 40 * 1 + 30 * 2 +5 * 4 + 10 * 4 = 205 。

输出描述

输出一个哈夫曼的中序遍历数组，数值间以空格分隔

示例：

模拟计算

请结合上图阅读！ 计算过程如下：

1. 输入的5个数是：5, 15, 40, 30, 10。
2. 将这些数作为节点值创建节点，并将节点添加到优先队列中。

3. 构建哈夫曼树：

   • 弹出两个最小的节点，值为5和10，合并为一个新节点值为15，将新节点添加回优先队列。
   • 弹出两个最小的节点，值为15（新合成的）和15（原始的），合并为一个新节点值为30，将新节点添加回优先队列。
   • 弹出两个最小的节点，值为30（新合成的）和30（原始的），合并为一个新节点值为60，将新节点添加回优先队列。
   • 弹出两个最小的节点，值为40和60，合并为一个新节点值为100，将新节点添加回优先队列。
   • 此时队列中只剩下一个节点，这就是树的根节点，值为100。

4. 对哈夫曼树进行中序遍历：

   • 访问左子树，值为40，它是一个叶子节点，输出40。
   • 访问根节点，值为100，输出100。

   • 访问右子树，值为60，它不是叶子节点，继续中序遍历：

     • 访问左子树，值为30，它不是叶子节点，继续中序遍历：

       • 访问左子树，值为15，它是一个叶子节点，输出15。
       • 访问根节点，值为30，输出30。
       • 访问右子树，值为15，它是一个叶子节点，输出15。
     • 访问根节点，值为60，输出60。

     • 访问右子树，值为30，它不是叶子节点，继续中序遍历：

       • 访问左子树，值为10，它是一个叶子节点，输出10。
       • 访问根节点，值为30，输出30。
       • 右子树为空，无输出。
5. 最终输出的结果是：40 100 15 30 60 10 30。

解题思路

小根堆（最小堆）：实现一个小根堆，用于在构建哈夫曼树的过程中维护节点的顺序，确保每次都能从中取出权值最小的节点。

贪心算法：构建哈夫曼树的过程本身是一个贪心算法的应用，每次选择两个权值最小的节点合并，以确保最终树的带权路径长度最短。

DFS（深度优先搜索）：在进行中序遍历时，使用了递归方法。

Python算法源码

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None  # 节点的左子节点
        self.right = None  # 节点的右子节点

class PriorityQueue:
    def __init__(self):
        self.data = []  # 存储队列元素的数组
  
    def push(self, node):
        self.data.append(node)
        self.data.sort(key=lambda x: x.value)  # 调整队列，保持最小堆的性质
  
    def pop(self):
        return self.data.pop(0)

def build_huffman_tree(values):
    pq = PriorityQueue()

    for value in values:
        pq.push(Node(value))

    while len(pq.data) > 1:
        left = pq.pop()  # 弹出最小元素作为左子节点
        right = pq.pop()  # 弹出下一个最小元素作为右子节点
        parent = Node(left.value + right.value)  # 创建新节点作为父节点
        parent.left = left   # 设置左子节点
        parent.right = right  # 设置右子节点
        pq.push(parent)  # 将新创建的父节点加入优先队列

    return pq.pop()  # 返回哈夫曼树的根节点

def inorder_traversal(root):
    if root:
        inorder_traversal(root.left)   # 遍历左子树
        print(root.value, end=" ")     # 打印节点值
        inorder_traversal(root.right)  # 遍历右子树

def main():
    n = int(input())  # 输入的节点数
    values = list(map(int, input().split()))  # 循环读取所有节点的值

    root = build_huffman_tree(values)  # 构建哈夫曼树
    inorder_traversal(root)  # 中序遍历哈夫曼树
    print()  # 打印换行

if __name__ == "__main__":
    main()

C算法源码

#include <stdio.h>
#include <stdlib.h>

// 定义节点结构体
typedef struct Node {
    int value; // 节点存储的数值
    struct Node* left; // 节点的左子节点
    struct Node* right; // 节点的右子节点
} Node;

// 创建节点的函数
Node* createNode(int value) {
    Node* node = (Node*)malloc(sizeof(Node));
    node->value = value;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 定义优先队列结构体
typedef struct PriorityQueue {
    Node** data; // 存储节点指针的数组
    int size; // 队列中节点的个数
    int capacity; // 队列的容量
} PriorityQueue;

// 创建优先队列的函数
PriorityQueue* createPriorityQueue(int capacity) {
    PriorityQueue* pq = (PriorityQueue*)malloc(sizeof(PriorityQueue));
    pq->data = (Node**)malloc(capacity * sizeof(Node*));
    pq->size = 0;
    pq->capacity = capacity;
    return pq;
}

// 交换两个节点指针的函数
void swap(Node** a, Node** b) {
    Node* temp = *a;
    *a = *b;
    *b = temp;
}

// 优先队列中插入节点的函数
void push(PriorityQueue* pq, Node* node) {
    pq->data[pq->size++] = node;
    // 调整队列，保持最小堆的性质
    int current = pq->size - 1;
    while (current > 0 && pq->data[current]->value < pq->data[(current - 1) / 2]->value) {
        swap(&pq->data[current], &pq->data[(current - 1) / 2]);
        current = (current - 1) / 2;
    }
}

// 优先队列中弹出节点的函数
Node* pop(PriorityQueue* pq) {
    if (pq->size == 0) return NULL;
    Node* popped = pq->data[0];
    pq->data[0] = pq->data[pq->size - 1];
    pq->size--;
    // 调整队列，保持最小堆的性质
    int current = 0;
    while (current * 2 + 1 < pq->size) {
        int smallest = current;
        int left = current * 2 + 1;
        int right = current * 2 + 2;
        if (left < pq->size && pq->data[left]->value < pq->data[smallest]->value) {
            smallest = left;
        }
        if (right < pq->size && pq->data[right]->value < pq->data[smallest]->value) {
            smallest = right;
        }
        if (smallest != current) {
            swap(&pq->data[current], &pq->data[smallest]);
            current = smallest;
        } else {
            break;
        }
    }
    return popped;
}

// 构建哈夫曼树的函数
Node* buildHuffmanTree(int values[], int n) {
    PriorityQueue* pq = createPriorityQueue(n);
    // 将输入的每个数值作为节点加入到优先队列中
    for (int i = 0; i < n; i++) {
        push(pq, createNode(values[i]));
    }
    // 循环处理，直到优先队列中只剩下一个节点
    while (pq->size > 1) {
        // 弹出两个数值最小的节点
        Node* left = pop(pq);
        Node* right = pop(pq);
        // 创建新节点，其数值为两个子节点数值之和
        Node* parent = createNode(left->value + right->value);
        // 设置新节点的左右子节点
        parent->left = left;
        parent->right = right;
        // 将新节点加入到优先队列中
        push(pq, parent);
    }
    // 返回优先队列中剩下的最后一个节点，即哈夫曼树的根节点
    return pop(pq);
}

// 中序遍历哈夫曼树的函数
void inorderTraversal(Node* root) {
    // 如果当前节点不为空，则进行遍历
    if (root != NULL) {
        // 递归遍历左子树
        inorderTraversal(root->left);
        // 访问当前节点，输出节点的值
        printf("%d ", root->value);
        // 递归遍历右子树
        inorderTraversal(root->right);
    }
}

int main() {
    // 读取第一个数字，表示后续将输入多少个数字
    int n;
    scanf("%d", &n);
    // 创建数组存储输入的数字
    int values[n];
    // 循环读取输入的数字并存储到数组中
    for (int i = 0; i < n; i++) {
        scanf("%d", &values[i]);
    }

    // 构建哈夫曼树，并返回根节点
    Node* root = buildHuffmanTree(values, n);
    // 对哈夫曼树进行中序遍历，并输出结果
    inorderTraversal(root);
    printf("\n"); // 打印换行

    return 0;
}

Java算法源码

import java.util.PriorityQueue;
import java.util.Scanner;

// 定义Node类，用于构建哈夫曼树的节点
class Node {
    int value; // 节点存储的数值
    Node left; // 节点的左子节点
    Node right; // 节点的右子节点
  
    // 构造函数，初始化节点的数值和左右子节点
    Node(int v) {
        value = v;
        left = null;
        right = null;
    }
}

// 比较器类，用于优先队列中比较Node对象
class Compare implements java.util.Comparator<Node> {
    // 重写compare方法，定义Node对象的比较规则
    public int compare(Node a, Node b) {
        // 返回a的数值是否大于b的数值
        return Integer.compare(a.value, b.value);
    }
}

// 构建哈夫曼树的方法
public class Main {
    public static Node buildHuffmanTree(int[] values) {
        // 创建优先队列，用于存储节点并按数值大小排序
        PriorityQueue<Node> pq = new PriorityQueue<>(new Compare());
        // 遍历数值数组，为每个数值创建一个节点并加入优先队列
        for (int value : values) {
            pq.add(new Node(value));
        }
        // 当优先队列中的节点数大于1时，执行循环
        while (pq.size() > 1) {
            // 取出两个数值最小的节点
            Node left = pq.poll();
            Node right = pq.poll();
            // 创建新节点，其数值为两个子节点数值之和
            Node parent = new Node(left.value + right.value);
            // 设置新节点的左右子节点
            parent.left = left;
            parent.right = right;
            // 将新节点加入到优先队列中
            pq.add(parent);
        }
        // 返回优先队列中剩下的最后一个节点，即哈夫曼树的根节点
        return pq.poll();
    }

    // 中序遍历哈夫曼树的方法
    public static void inorderTraversal(Node root, StringBuilder result) {
        if (root != null) {
            // 递归遍历左子树
            inorderTraversal(root.left, result);
            // 访问当前节点，将数值转为字符串并追加到结果字符串中
            result.append(root.value).append(" ");
            // 递归遍历右子树
            inorderTraversal(root.right, result);
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(); // 从标准输入读取n的值
        int[] values = new int[n]; // 创建一个整数数组，用于存储输入的数值
        // 循环读取n个数值，并存储到数组values中
        for (int i = 0; i < n; ++i) {
            values[i] = scanner.nextInt();
        }

        // 调用buildHuffmanTree方法构建哈夫曼树，并获取根节点
        Node root = buildHuffmanTree(values);
        StringBuilder result = new StringBuilder(); // 创建一个字符串构建器，用于存储中序遍历的结果
        // 调用inorderTraversal方法进行中序遍历，并将结果存储到result中
        inorderTraversal(root, result);
        // 移除最后一个空格
        if (result.length() > 0) {
            result.deleteCharAt(result.length() - 1);
        }
        // 输出中序遍历的结果
        System.out.println(result);
    }
}