返回目录
题目描述
推荐多样性需要从多个列表中选择元素,一次性要返回 N 屏数据(窗口数量),每屏展示 K 个元素(窗口大小),选择策略:
- 各个列表元素需要做穿插处理,即先从第一个列表中为每屏选择一个元素,再从第二个列表中为每屏选择一个元素,依次类推
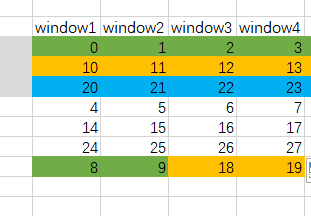
每个列表的元素尽量均分为 N 份,如果不够 N 个,也要全部分配完,参考样例图:
(1)从第一个列表中选择 4 条 0 1 2 3,分别放到 4 个窗口中
(2)从第二个列表中选择 4 条 10 11 12 13,分别放到 4 个窗口中
(3)从第三个列表中选择 4 条 20 21 22 23,分别放到 4 个窗口中
(4)再从第一个列表中选择 4 条 4 5 6 7,分别放到 4 个窗口中
(5)再从第一个列表中选择,由于数量不足 4 条,取剩下的 2 条,放到 窗口1 和 窗口2
(6)再从第二个列表中选择,由于数量不足 4 条并且总的元素数达到窗口要求,取 18 19 放到 窗口3 和 窗口4
输入 
处理
输出

输入描述
第一行输入为 N,表示需要输出的窗口数量,取值范围 [1, 10]
第二行输入为 K,表示每个窗口需要的元素数量,取值范围 [1, 100]
之后的行数不定(行数取值范围 [1, 10]),表示每个列表输出的元素列表。元素之间以空格隔开,已经过排序处理,每个列表输出的元素数量取值范围 [1, 100]
输出描述
输出元素列表,元素数量 = 窗口数量 * 窗口大小,元素之间以空格分隔,多个窗口合并为一个列表输出,参考样例:
先输出窗口1的元素列表,再输出窗口2的元素列表,再输出窗口3的元素列表,最后输出窗口4的元素列表
备注
- 每个列表会保证元素数量满足窗口要求,不需要考虑元素不足情况
- 每个列表的元素已去重,不需要考虑元素重复情况
- 每个列表的元素列表均不为空,不需要考虑列表为空的情况
- 每个列表的元素列表已经过排序处理,输出结果要保证不改变同一个列表的元素顺序
- 每个列表的元素数量可能是不同的
示例:
| 输入 | 4 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
|---|---|
| 输出 | 0 10 20 4 14 24 8 1 11 21 5 15 25 9 2 12 22 6 16 26 18 3 13 23 7 17 27 19 |
| 说明 | 无 |
题目解析
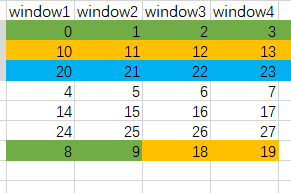
我们可以将最终的窗口集当成一个矩阵windows,该矩阵有 k 行 n 列,矩阵的每一列对应一个窗口。最终按列打印该矩阵,即为题解。
Python算法源码
# Python 代码
def main():
n = int(input())
k = int(input())
lists = []
while True:
line = input().strip()
# 本地测试,以空行作为输入截止条件
if not line:
break
nums = list(map(int, line.split(" ")))
lists.append(nums)
# 窗口矩阵,k行n列,每一列对应一个窗口,这里将二维矩阵一维化,方便后面赋值
windows = [0] * (k * n)
# 窗口矩阵中正在赋值的索引位置
idx = 0
# 正在从第level个列表中取值
level = 0
# 当窗口矩阵填满后,结束循环
while idx < len(windows):
# 当前轮次是否发生了"借"动作
flag = False
# 从第level个列表中取前n个元素
for i in range(n):
windows[idx] = lists[level].pop(0)
idx += 1
# 如果第level个列表没有元素了,则继续切到下一个列表中"借"
if len(lists[level]) == 0 and len(lists) > 1:
lists.pop(level) # 删除空列表
level %= len(lists) # 防止越界
flag = True # 发生了"借"动作
# 如果没有发生"借"动作,则需要切到下一行
if not flag:
level = (level + 1) % len(lists) # 防止越界
result = []
# 遍历窗口矩阵的每一列
for j in range(n): # 遍历列号
for i in range(k): # 遍历行号
result.append(str(windows[i * n + j])) # 将每一列的元素进行拼接
print(" ".join(result))
if __name__ == "__main__":
main()C算法源码
# 输入获取
n = int(input())
k = int(input())
lists = []
while True:
try:
lists.append(list(map(int, input().split())))
except:
break
# 算法入口
def getResult():
# 窗口矩阵,k行n列,每一列对应一个窗口,这里将二维矩阵一维化,方便后面赋值
windows = [0] * (k * n)
# 窗口矩阵中正在赋值的索引位置
idx = 0
# 正在从第level个列表中取值
level = 0
# 当窗口矩阵填满后,结束循环
while idx < len(windows):
# 当前轮次是否发生了"借"动作
flag = False
# 从第level个列表中取前n个元素
for _ in range(n):
windows[idx] = lists[level].pop(0)
idx += 1
# 如果第level个列表没有元素了,则继续切到下一个列表中"借"
if len(lists[level]) == 0 and len(lists) > 1:
lists.pop(level) # 删除空列表
level %= len(lists) # 防止越界
flag = True # 发生了"借"动作
# 如果没有发生"借"动作,则需要切到下一行
if not flag:
level = (level + 1) % len(lists) # 防止越界
ans = []
# 遍历列号
for j in range(n):
# 遍历行号
for i in range(k):
# 按列收集元素
ans.append(windows[i * n + j])
return " ".join(map(str, ans))
# 算法调用
print(getResult())Java算法源码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
int k = Integer.parseInt(sc.nextLine());
ArrayList<LinkedList<Integer>> lists = new ArrayList<>();
while (sc.hasNextLine()) {
String line = sc.nextLine();
// 本地测试,以空行作为输入截止条件
if (line.length() == 0) break;
Integer[] nums =
Arrays.stream(line.split(" ")).map(Integer::parseInt).toArray(Integer[]::new);
lists.add(new LinkedList<>(Arrays.asList(nums)));
}
int[] windows = new int[k * n];
int idx = 0;
int level = 0;
while (idx < windows.length) {
boolean flag = false;
for (int i = 0; i < n; i++) {
windows[idx++] = lists.get(level).removeFirst();
if (lists.get(level).size() == 0 && lists.size() > 1) {
lists.remove(level);
level %= lists.size();
flag = true;
}
}
if (!flag) {
level = (level + 1) % lists.size();
}
}
StringJoiner sj = new StringJoiner(" ");
for (int j = 0; j < n; j++) {
for (int i = 0; i < k; i++) {
sj.add(windows[i * n + j] + "");
}
}
System.out.println(sj);
}
}
此处评论已关闭