返回目录
题目描述
在某个项目中有多个任务(用task数组表示)需要你进行处理,其中:
- task[i] = [si, ei]
你可以在 si ≤ day ≤ ei 中的任意一天处理该任务,请返回你可以处理的最大任务数。
输入描述
第一行为任务数量 n
- 1 ≤ n ≤ 100000
后面 n 行表示各个任务的开始时间和终止时间,使用 si,ei 表示
- 1 ≤ si ≤ ei ≤ 100000
输出描述
输出为一个整数,表示可以处理的最大任务数。
示例:
| 输入 | 3 1 1 1 2 1 3 |
|---|---|
| 输出 | 3 |
| 说明 | 无 |
题目解析
本题可以利用贪心思维+优先队列来求解。
我们可以将所有任务时间区间按照:优先按照结束时间降序,如果结束时间相同,则按照开始时间降序。这样排序的原因如下:
首先,任务优先按照结束时间降序后,那么第一个任务的结束时间就是最晚的(最大的),此时我们可以让第一个任务就在最晚时刻执行,如下面例子:
3
1 4
2 3
1 2
按照结束时间降序后:[1,4] , [2, 3], [1, 2] ,第一个任务[1,4]在时刻4执行
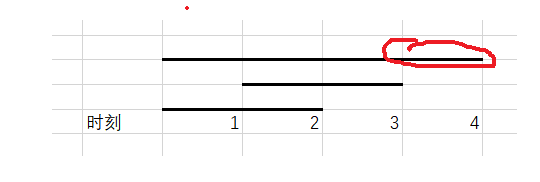
这样做的好处是,避免第一个任务抢夺后面任务的执行时间,如下图所示:
- 如果第一个任务在时刻4执行,则第二个任务就有两个选择,时刻2或时刻3
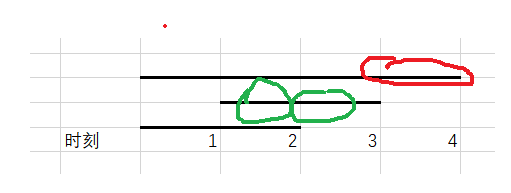
- 如果第一个任务在时刻3执行,则第二个任务就只有一个选择,只能在时刻2执行
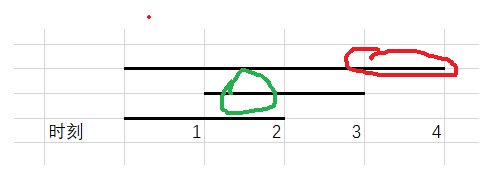
如果存在多个任务的结束时间都相同的话,则还需要对这些任务按照开始时间降序,这么做的原因是:
- "时间长" 的任务 "可选执行时刻" 多
- "时间短" 的任务 "可选执行时刻" 少
因此应该优先让时间跨度短的任务先执行,如下图所示:
- 如果优先时间短的任务,则三个任务都能执行
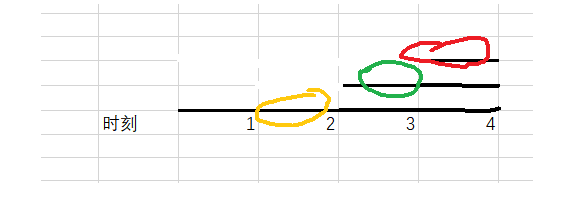
- 如果优先时间长的任务,则只能执行两个任务
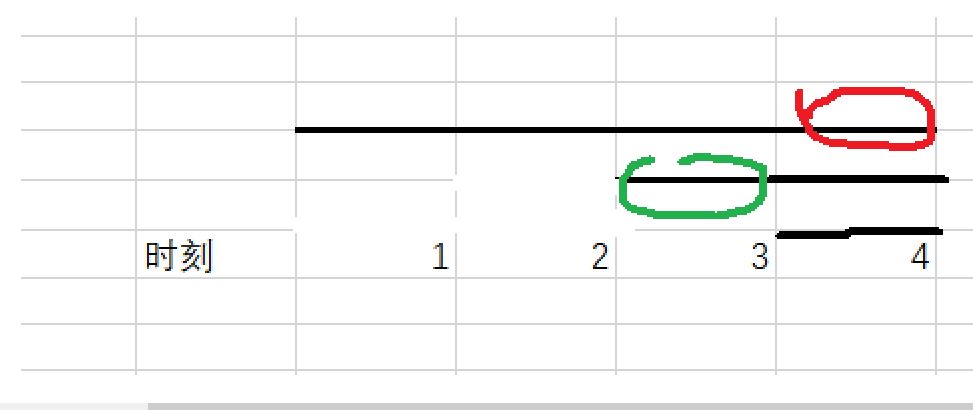
但是上面逻辑是存在问题的,请看下面图示:
此时按照前面逻辑的话,只能执行三个任务
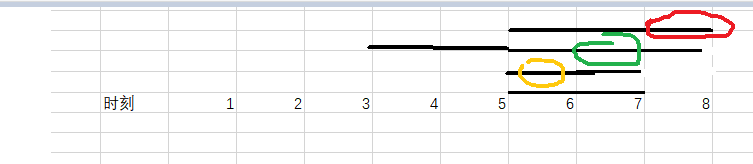
但是其实可以执行四个任务,执行策略如下: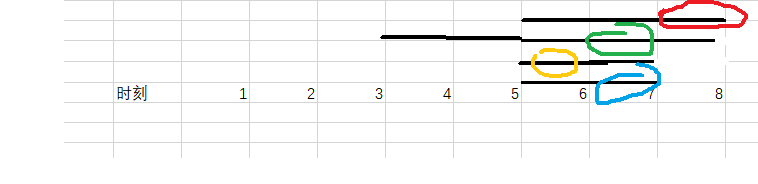
主要问题是,当我们按照结束时间降序后,第一个任务选择时刻8执行完,此时后面三个任务的截止时间其实都是相同的,变为了时刻7。
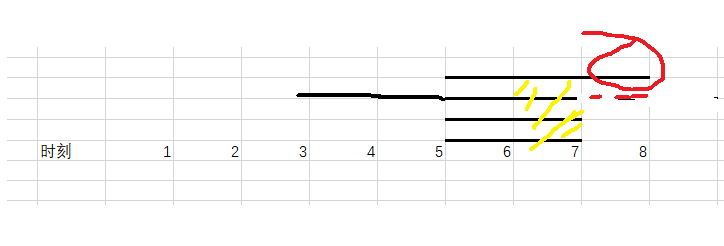
因此,此时我们应该对后面三个任务重新按照时间跨度降序,再优先执行短的任务。
本题数量级较大,因此如果每次执行完一个任务,都对剩余任务进行更新结束时间,并重新排序的话,会超时。
改进策略是,使用优先队列,即:
如果当前任务的结束时间end >= 上一个任务的执行时刻last\_end,则更新当前任务的结束为last\_end - 1。如果 last\_end - 1 > 当前任务开始时间start,则将当前任务重新入队排优先级。否则当前任务不可执行。
Python算法源码
import heapq
n = int(input())
ranges = []
for _ in range(n):
start, end = map(int, input().split())
ranges.append((end, start)) # 存储为(end, start)元组,便于使用优先队列处理结束时间相同的任务
# 按照结束时间降序排序
ranges.sort(reverse=True)
pq = [] # 优先队列
pq_end = float('inf') # 优先队列中任务的相同结束时间
count = 0 # 最大任务数
for end, start in ranges:
# 处理结束时间相同的任务
while pq and end < pq_end:
if heapq.heappop(pq) <= pq_end:
count += 1
pq_end -= 1
# 添加任务的开始时间到优先队列
heapq.heappush(pq, start)
pq_end = end
# 处理剩余任务
while pq:
if heapq.heappop(pq) <= pq_end:
count += 1
pq_end -= 1
print(count)C语言算法源码
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
// 定义元素类型为整型
typedef int E;
/* 优先队列实现 */
typedef struct PriorityQueue {
E *data; // 存储队列元素的数组
int size; // 队列当前元素个数
int (*compare)(E, E); // 比较函数指针,用于定义元素优先级
} PQ;
// 创建一个新的优先队列
PQ *new_PriorityQueue(int capacity, int (*cmp_func)(E, E)) {
PQ *pq = (PQ *) malloc(sizeof(PQ)); // 分配内存空间
pq->data = (E *) malloc(sizeof(E) * capacity); // 分配存储数据的空间
pq->size = 0; // 初始化队列元素个数为0
pq->compare = cmp_func; // 设置比较函数
return pq;
}
// 交换队列中两个元素的位置
void swap_PQ(PQ *pq, int a, int b) {
E temp = pq->data[a];
pq->data[a] = pq->data[b];
pq->data[b] = temp;
}
// 元素上浮操作
void swim_PQ(PQ *pq) {
int child_index = pq->size - 1;
while (child_index >= 1) {
int parent_index = (child_index - 1) / 2; // 计算父节点索引
if (pq->compare(pq->data[child_index], pq->data[parent_index]) < 0) {
swap_PQ(pq, child_index, parent_index); // 子节点比父节点小,则交换
child_index = parent_index; // 更新子节点索引为父节点索引
} else {
break; // 否则退出循环
}
}
}
// 入队操作
void offer_PQ(PQ *pq, E val) {
pq->data[pq->size++] = val; // 将元素放入队尾
swim_PQ(pq); // 进行上浮操作
}
// 元素下沉操作
void sink_PQ(PQ *pq) {
int parent_index = 0;
while (1) {
int left_child_index = 2 * parent_index + 1; // 计算左子节点索引
int right_child_index = left_child_index + 1; // 计算右子节点索引
int child_index; // 存储较小(优先级较高)子节点索引
// 选择较小(优先级较高)的子节点
if (pq->size > right_child_index && pq->compare(pq->data[right_child_index], pq->data[left_child_index]) < 0) {
child_index = right_child_index;
} else {
child_index = left_child_index;
}
// 如果父节点比较小(优先级较高),则交换父节点和子节点位置
if (pq->size > child_index && pq->compare(pq->data[child_index], pq->data[parent_index]) < 0) {
swap_PQ(pq, child_index, parent_index);
parent_index = child_index; // 更新父节点索引为子节点索引
} else {
break; // 否则退出循环
}
}
}
// 出队操作
E poll_PQ(PQ *pq) {
swap_PQ(pq, 0, pq->size - 1); // 将队首元素与队尾元素交换
E result = pq->data[--pq->size]; // 取出队尾元素
sink_PQ(pq); // 进行下沉操作
return result; // 返回出队的元素
}
// 比较函数,用于qsort排序
int compare(const void *a, const void *b) {
int *A = (int *) a;
int *B = (int *) b;
return B[1] - A[1]; // 按结束时间降序排列
}
// 优先队列的比较函数
int compare_PQ(int a, int b) {
return b - a; // 返回b-a的结果,即b大于a时返回正数
}
int main() {
int num_tasks;
scanf("%d", &num_tasks); // 输入任务数
int tasks[num_tasks][2]; // 存储任务的开始和结束时间
// 输入任务的开始和结束时间
for (int i = 0; i < num_tasks; i++) {
scanf("%d %d", &tasks[i][0], &tasks[i][1]);
}
// 按结束时间降序排序任务数组
qsort(tasks, num_tasks, sizeof(tasks[0]), compare);
// 创建优先队列,用于存储任务的开始时间
PQ *priority_queue = new_PriorityQueue(num_tasks, compare_PQ);
int pq_end_time = INT_MAX; // 记录优先队列中任务的最晚结束时间
int num_processed_tasks = 0; // 记录已处理的任务数量
for (int i = 0; i < num_tasks; i++) {
int start_time = tasks[i][0]; // 当前任务的开始时间
int end_time = tasks[i][1]; // 当前任务的结束时间
// 处理紧急任务
while (priority_queue->size > 0 && end_time < pq_end_time) {
if (poll_PQ(priority_queue) <= pq_end_time) {
num_processed_tasks++; // 处理任务数量加一
pq_end_time--; // 一个时刻只能执行一个任务,结束时间减一
}
}
offer_PQ(priority_queue, start_time); // 将当前任务的开始时间加入优先队列
pq_end_time = end_time; // 更新优先队列中任务的最晚结束时间
}
// 处理剩余的任务
while (priority_queue->size > 0) {
if (poll_PQ(priority_queue) <= pq_end_time) {
num_processed_tasks++;
pq_end_time--;
}
}
printf("%d\n", num_processed_tasks); // 输出处理的任务数量
return 0;
}Java算法源码
# 计算两个数字的和
result = num1 + num2
# 检查用户输入是否为正数
if num > 0:
# 如果是正数,输出结果
print("The number is positive.")
else:
# 如果不是正数,输出错误信息
print("The number is not positive.")
# 使用 for 循环遍历列表
for item in my_list:
# 打印列表中的每个元素
print(item)
# 定义一个函数,计算两个数的乘积
def multiply(x, y):
"""
This function takes two numbers as input and returns their product.
"""
return x * y
3 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]