返回目录

题目描述

宝宝和妈妈参加亲子游戏，在一个二维矩阵（N*N）的格子地图上，宝宝和妈妈抽签决定各自的位置，地图上每个格子有不同的糖果数量，部分格子有障碍物。

游戏规则是妈妈必须在最短的时间（每个单位时间只能走一步）到达宝宝的位置，路上的所有糖果都可以拿走，不能走障碍物的格子，只能上下左右走。

请问妈妈在最短到达宝宝位置的时间内最多拿到多少糖果（优先考虑最短时间到达的情况下尽可能多拿糖果）。

输入描述

第一行输入为 N，N 表示二维矩阵的大小

之后 N 行，每行有 N 个值，表格矩阵每个位置的值，其中：

• -3：妈妈
• -2：宝宝
• -1：障碍
• ≥0：糖果数（0表示没有糖果，但是可以走）

输出描述

输出妈妈在最短到达宝宝位置的时间内最多拿到多少糖果，行末无多余空格

备注

地图最大 50*50

示例：

输入	4 3 2 1 -3 1 -1 1 1 1 1 -1 2 -2 1 2 3
输出	9
说明	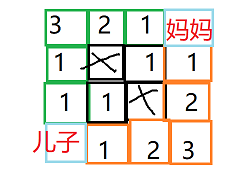此地图有两条最短路径可到达宝宝位置，绿色线和黄色线都是最短路径6步， 但黄色拿到的糖果更多，9个。

输入	4 3  2  1  -3 -1 -1 1 1 1 1 -1  23 2 1 -2 1 -1 3
输出	-1
说明	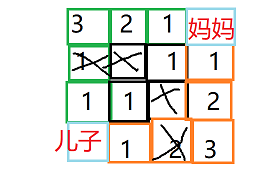此地图妈妈无法到达宝宝位置

题目解析

本题需要我们优先找到妈妈到宝宝的最短路径，如果存在多条最短路径的话，则选择其中能拿到最多糖果数的路径。

那么如何求解妈妈到宝宝的最短路径呢？

其实很简单，就是单纯的BFS按层扩散，比如下图所示：

此时将妈妈位置作为源点，开始按层扩散

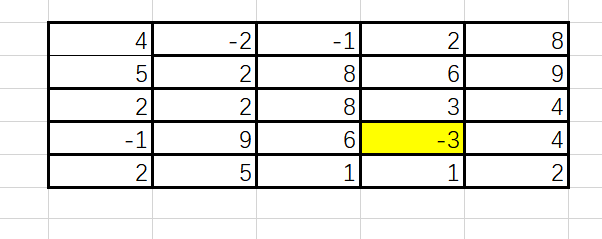
扩散到第一层

扩散第二层

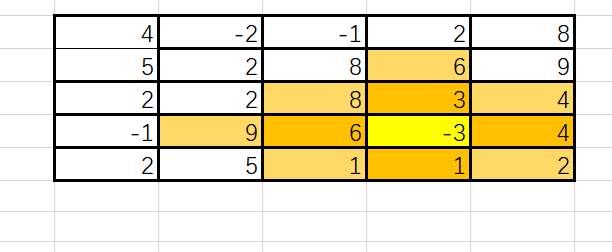
扩散到第三层

扩散到第四层

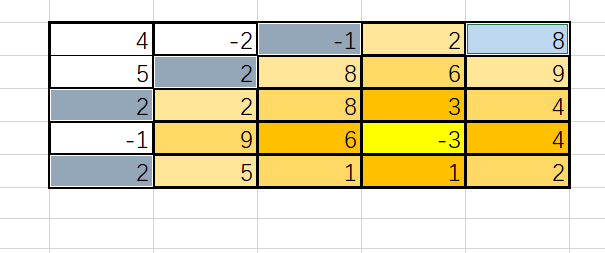
扩散到第五层，此时扩散到了宝宝位置，也就是说妈妈到宝宝位置的最短距离是五步。

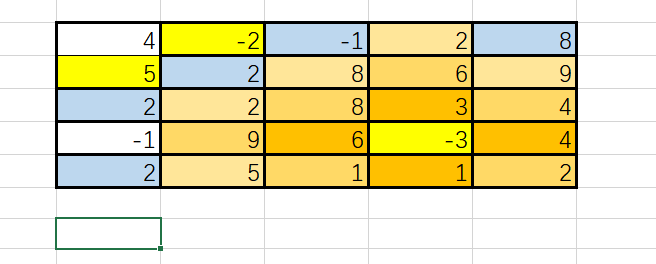
Python算法源码

from collections import deque

# 定义全局变量n和matrix
n = int(input())
matrix = []

# 初始化candy矩阵
candy = [[-1] * n for _ in range(n)]

# 定义偏移量
offsets = [(1, 0), (0, -1), (-1, 0), (0, 1)]

# 读取地图矩阵
for _ in range(n):
    row = list(map(int, input().split()))
    matrix.append(row)

    # 初始化妈妈的位置并加入队列
    if -3 in row:
        start_pos = (len(matrix) - 1, row.index(-3))
        candy[start_pos[0]][start_pos[1]] = 0
        queue = deque([start_pos])

# 记录题解
ans = -1

# bfs 按层扩散
while queue:
    # 记录当前扩散层的点
    new_queue = deque()

    # 当前层是否有宝宝所在的点
    flag = False

    for pos in queue:
        x, y = pos

        # 向四个方向扩散
        for offset in offsets:
            new_x = x + offset[0]
            new_y = y + offset[1]

            # 当前扩散点坐标越界，或者扩散点是墙，则无法扩散
            if new_x < 0 or new_x >= n or new_y < 0 or new_y >= n or matrix[new_x][new_y] == -1:
                continue

            # 当前扩散点坐标对应的糖果数量为-1，说明对应扩散点坐标位置还没有加入到当前扩散层
            if candy[new_x][new_y] == -1:
                new_queue.append((new_x, new_y))

            # 当前扩散点可能会被多个源点扩散到，因此比较保留扩散过程中带来的较大糖果数
            # candy[new_x][new_y] 记录的是当前扩散点获得的糖果数
            # candy[x][y] + max(0, matrix[new_x][new_y]) 记录的是从源点(x,y)带来的糖果数 + (new_x,new_y)位置原本的糖果数
            candy[new_x][new_y] = max(candy[new_x][new_y], candy[x][y] + max(0, matrix[new_x][new_y]))

            # 如果当前扩散点是宝宝位置，则可以停止后续层级的bfs扩散，因为已经找到宝宝的最短路径长度（即扩散层数）
            if matrix[new_x][new_y] == -2:
                ans = candy[new_x][new_y]
                flag = True

    # 已经找到去宝宝位置的最短路径和最大糖果数，则终止bfs
    if flag:
        break

    # 否则继续
    queue = new_queue

print(ans)

C算法源码

#include <stdio.h>
#include <stdbool.h>

int max(int a, int b) {
    return a > b ? a : b;
}

int main() {
    int n;
    scanf("%d", &n);

    int matrix[n][n];
    int candy[n][n];

    int offsets[4][2] = {{1, 0},
                         {-1, 0},
                         {0, -1},
                         {0, 1}};

    int queue[n*n];
    int front = 0, rear = 0;

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            candy[i][j] = -1;

            scanf("%d", &matrix[i][j]);

            if (matrix[i][j] == -3) {
                candy[i][j] = 0;
                queue[rear++] = i * n + j;
            }
        }
    }

    int ans = -1;

    while (front != rear) {
        int newQueue[n*n];
        int newRear = 0;

        bool flag = false;

        while (front != rear) {
            int pos = queue[front++];

            int x = pos / n;
            int y = pos % n;

            for (int k = 0; k < 4; k++) {
                int newX = x + offsets[k][0];
                int newY = y + offsets[k][1];

                if (newX < 0 || newX >= n || newY < 0 || newY >= n || matrix[newX][newY] == -1) continue;

                if (candy[newX][newY] == -1) {
                    newQueue[newRear++] = newX * n + newY;
                }

                candy[newX][newY] = max(candy[newX][newY], candy[x][y] + (matrix[newX][newY] > 0 ? matrix[newX][newY] : 0));

                if (matrix[newX][newY] == -2) {
                    ans = candy[newX][newY];
                    flag = true;
                }
            }
        }

        if (flag) break;

        for (int i = 0; i < newRear; i++) {
            queue[i] = newQueue[i];
        }
        front = 0;
        rear = newRear;
    }

    printf("%d\n", ans);

    return 0;
}

Java算法源码

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Scanner;

public class Main {

    static class Point {
        int x; // 横坐标
        int y; // 纵坐标

        public Point(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(); // 读取网格大小

        // 初始化网格矩阵和糖果矩阵
        int[][] matrix = new int[n][n];
        int[][] candy = new int[n][n];

        // 定义四个方向的偏移量（右、左、上、下）
        int[][] offsets = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};

        // 用于存储糖果位置的队列
        Deque<Point> queue = new ArrayDeque<>();

        // 读取网格并初始化糖果位置
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                candy[i][j] = -1; // 将糖果数组初始化为-1
                matrix[i][j] = scanner.nextInt(); // 读取网格值

                // 如果单元格中包含糖果，初始化糖果数组并将其添加到队列中
                if (matrix[i][j] == -3) {
                    candy[i][j] = 0;
                    queue.addLast(new Point(i, j));
                }
            }
        }

        int ans = -1; // 初始化答案为-1

        // 广度优先搜索（BFS）以找到收集的最大糖果数
        while (!queue.isEmpty()) {
            Deque<Point> newQueue = new ArrayDeque<>(); // 初始化下一层BFS的新队列
            boolean flag = false; // 标志以检查是否到达目标位置

            // 遍历当前队列中的每个位置
            for (Point pos : queue) {
                int x = pos.x;
                int y = pos.y;

                // 遍历四个方向
                for (int[] offset : offsets) {
                    int newX = x + offset[0];
                    int newY = y + offset[1];

                    // 检查新位置是否在网格边界内且不是障碍物
                    if (newX < 0 || newX >= n || newY < 0 || newY >= n || matrix[newX][newY] == -1)
                        continue;

                    // 如果新位置上的糖果未被访问，则将其添加到新队列中
                    if (candy[newX][newY] == -1) {
                        newQueue.addLast(new Point(newX, newY));
                    }

                    // 更新新位置上收集的最大糖果数
                    candy[newX][newY] = Math.max(candy[newX][newY], candy[x][y] + Math.max(0, matrix[newX][newY]));

                    // 如果到达目标位置，更新答案并设置标志
                    if (matrix[newX][newY] == -2) {
                        ans = candy[newX][newY];
                        flag = true;
                    }
                }
            }

            // 如果到达目标位置，则跳出循环
            if (flag) break;

            // 更新下一层BFS的队列
            queue = newQueue;
        }

        // 输出收集的最大糖果数
        System.out.println(ans);
    }
}