返回目录
题目描述
园区某部门举办了Family Day,邀请员工及其家属参加;
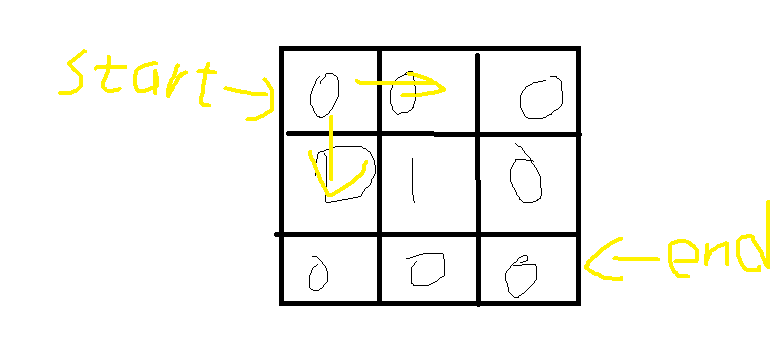
将公司园区视为一个矩形,起始园区设置在左上角,终点园区设置在右下角;
家属参观园区时,只能向右和向下园区前进,求从起始园区到终点园区会有多少条不同的参观路径。
输入描述
第一行为园区的长和宽;
后面每一行表示该园区是否可以参观,0表示可以参观,1表示不能参观
输出描述
输出为不同的路径数量
示例:
| 输入 | 3 3 0 0 0 0 1 0 0 0 0 |
|---|---|
| 输出 | 2 |
| 说明 | 无 |
题目解析
本题如果地图矩阵数量级过大的话,深搜解题会超时。因此,更优解法是利用动态规划,我们可以定义一个dp二维数组,dpi的含义是:从坐标(0,0)到达坐标(i, j)的路径数
而本题说只能向下或者向右运动,因此到达一个坐标点,可能来自其上方,亦可能来自其左方
因此 dpi = dpi-1 + dpi
即:
如果到达(i-1,j)的路径有dpi-1条,那么到达(i,j)的路径也有dpi-1条
同理到达(i, j-1)的路径有dpi,那么到达(i,j)的路径也有dpi条
因此:dpi = dpi-1 + dpi
Python算法源码
# 读取输入
n, m = map(int, input().split())
# 读取地图矩阵
matrix = []
for i in range(n):
row = list(map(int, input().split()))
matrix.append(row)
# 如果起点或终点为障碍物,无解
if matrix[0][0] == 1 or matrix[n - 1][m - 1] == 1:
print("0")
exit()
# 初始化dp数组
dp = [[0] * m for _ in range(n)]
dp[0][0] = 1
# 动态规划求解
for i in range(n):
for j in range(m):
if matrix[i][j] == 1:
continue
if i > 0:
dp[i][j] += dp[i - 1][j]
if j > 0:
dp[i][j] += dp[i][j - 1]
# 输出结果
print(dp[n - 1][m - 1])C算法源码
#include <stdio.h>
int main() {
// 创建输入扫描器
int n, m;
scanf("%d %d", &n, &m);
// 创建地图矩阵
int matrix[n][m];
// 读取地图矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
scanf("%d", &matrix[i][j]);
}
}
// 如果起点和终点不能参观,则没有路径
if (matrix[0][0] == 1 || matrix[n - 1][m - 1] == 1) {
printf("0\n");
return 0;
}
// 初始化dp数组
long dp[n][m];
dp[0][0] = 1;
// 动态规划求解
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j] == 1) {
continue;
}
if (i > 0) {
dp[i][j] += dp[i - 1][j];
}
if (j > 0) {
dp[i][j] += dp[i][j - 1];
}
}
}
// 输出结果
printf("%ld\n", dp[n - 1][m - 1]);
return 0;
}java算法源码
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// 创建输入扫描器
Scanner scanner = new Scanner(System.in);
// 读取输入,获取地图行数和列数
int n = scanner.nextInt();
int m = scanner.nextInt();
// 创建地图矩阵
int[][] matrix = new int[n][m];
// 读取地图矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
matrix[i][j] = scanner.nextInt();
}
}
// 如果起点或终点为障碍物,无解
if (matrix[0][0] == 1 || matrix[n - 1][m - 1] == 1) {
System.out.println("0");
return;
}
// 初始化dp数组
long[][] dp = new long[n][m];
dp[0][0] = 1;
// 动态规划求解
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j] == 1) {
continue;
}
if (i > 0) {
dp[i][j] += dp[i - 1][j];
}
if (j > 0) {
dp[i][j] += dp[i][j - 1];
}
}
}
// 输出结果
System.out.println(dp[n - 1][m - 1]);
}
}
3 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]