返回目录
题目描述
一个局域网内有很多台电脑,分别标注为 0 \~ N-1 的数字。相连接的电脑距离不一样,所以感染时间不一样,感染时间用 t 表示。
其中网络内一台电脑被病毒感染,求其感染网络内所有的电脑最少需要多长时间。如果最后有电脑不会感染,则返回-1。
给定一个数组 times 表示一台电脑把相邻电脑感染所用的时间。
如图:path[i] = {i, j, t} 表示:电脑 i->j,电脑 i 上的病毒感染 j,需要时间 t。
输入描述
4
3
2 1 1
2 3 1
3 4 1
2
输出描述
2
示例:
| 输入 | 4 3 2 1 1 2 3 1 3 4 1 2 |
|---|---|
| 输出 | 2 |
| 说明 | 第一个参数:局域网内电脑个数N,1 ≤ N ≤ 200; 第二个参数:总共多少条网络连接 第三个 2 1 1 表示2->1时间为1 第六行:表示病毒最开始所在电脑号2 |
题目解析
用例图示如下
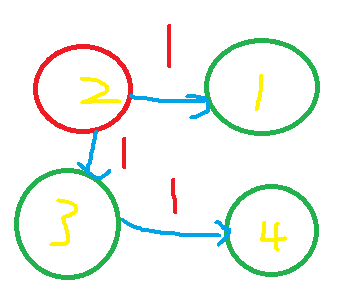
病毒源头是2,其中:
2->1需要时间1
2->3需要时间1,3->4需要时间1
因此最少需要时间2才能感染所有电脑。
Python算法源码
import heapq
def getMinTime(n, m, graph, start):
dist = [float('inf')] * (n + 1)
dist[0] = 0
dist[start] = 0
need_check = []
heapq.heappush(need_check, start)
visited = [False] * (n + 1)
visited[start] = True
while need_check:
cur = heapq.heappop(need_check)
visited[cur] = False
if cur in graph:
for v, w in graph[cur]:
new_dist = dist[cur] + w
if dist[v] > new_dist:
dist[v] = new_dist
if not visited[v]:
visited[v] = True
heapq.heappush(need_check, v)
ans = max(dist)
return -1 if ans == float('inf') else ans
if __name__ == "__main__":
n = int(input())
graph = {}
m = int(input())
for _ in range(m):
u, v, w = map(int, input().split())
if u not in graph:
graph[u] = []
graph[u].append((v, w))
start = int(input())
result = getMinTime(n, m, graph, start)
print(result)C算法源码
#include <stdio.h>
#include <limits.h>
#define MAX_NODES 1000
#define MAX_EDGES 1000
int getMinTime(int n, int m, int path[][3], int start) {
int time[MAX_NODES + 1];
for (int i = 0; i <= n; i++)
time[i] = INT_MAX;
time[0] = 0;
time[start] = 0;
for (int i = 0; i < n - 1; i++) {
int flag = 0;
for (int j = 0; j < m; j++) {
int u = path[j][0];
int v = path[j][1];
int t = path[j][2];
if (time[u] != INT_MAX && time[v] > time[u] + t) {
time[v] = time[u] + t;
flag = 1;
}
}
if (!flag)
break;
}
int max = INT_MIN;
for (int i = 0; i <= n; i++) {
if (time[i] > max)
max = time[i];
}
return max == INT_MAX ? -1 : max;
}
int main() {
int n, m;
scanf("%d %d", &n, &m);
int path[MAX_EDGES][3];
for (int i = 0; i < m; i++) {
scanf("%d %d %d", &path[i][0], &path[i][1], &path[i][2]);
}
int start;
scanf("%d", &start);
int result = getMinTime(n, m, path, start);
printf("%d\n", result);
return 0;
}Java算法源码
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
// 邻接表
HashMap<Integer, ArrayList<int[]>> graph = new HashMap<>();
int m = sc.nextInt();
for (int i = 0; i < m; i++) {
int u = sc.nextInt(); // 出发点
int v = sc.nextInt(); // 目标点
int w = sc.nextInt(); // 出发点到达目标点的耗时
graph.putIfAbsent(u, new ArrayList<>());
graph.get(u).add(new int[]{v, w});
}
// 记录源点到其他各点的最短耗时
// 初始时,假设源点不可达其他剩余点,即源点到达其他点的耗时无限大
int[] dist = new int[n + 1];
Arrays.fill(dist, Integer.MAX_VALUE);
// 源点
int src = sc.nextInt();
// 源点到达源点的耗时为0
dist[src] = 0;
// needCheck中记录的其实是:已被探索过的路径的终点(路径指的是源点->终点)
// 排序规则是,路径终点的权重(即源点->终点的耗时)越小越靠后
// 初始被探索过的路径只有源点本身
PriorityQueue<Integer> needCheck = new PriorityQueue<>((a, b) -> dist[b] - dist[a]);
needCheck.add(src);
// 记录对应点是否在needCheck中
boolean[] visited = new boolean[n + 1];
visited[src] = true;
while (!needCheck.isEmpty()) {
// 取出最优路径的终点(耗时最少的路径)作为新的起点
int cur = needCheck.poll();
visited[cur] = false;
// 如果cur有可达的其他点
if (graph.containsKey(cur)) {
// v是可达的其他店,w是cur->v的耗时
for (int[] next : graph.get(cur)) {
int v = next[0], w = next[1];
// 那么如果从源点到cur点的耗时是dist[cur],那么源点到v点的耗时就是dist[cur] + w
int newDist = dist[cur] + w;
// 而源点到v的耗时之前是dist[v],因此如果newDist < dist[v],则找到更少耗时的路径
if (dist[v] > newDist) {
// 更新源点到v的路径,即更新v点权重
dist[v] = newDist;
// 如果v点不在needCheck中,则加入,因为v作为终点的路径需要加入到下一次最优路径的评比中
if (!visited[v]) {
visited[v] = true;
needCheck.add(v);
}
}
}
}
}
int ans = Integer.MIN_VALUE;
for (int i = 1; i <= n; i++) {
ans = Math.max(ans, dist[i]);
}
// dist记录的是源点到达其他各点的最短耗时,我们取出其中最大的就是源点走完所有点的最短耗时
System.out.println(ans == Integer.MAX_VALUE ? -1 : ans);
}
}
4 条评论
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]2024 C卷 100分序号题目知 识 点难易程度1密码输入检测数据结构/栈☆☆☆2分配土地几何问题☆☆☆3找座位逻辑分析☆☆☆4智能成绩表动态条件分析☆☆☆5内存冷热标记多条件排序☆☆☆6螺旋数字矩阵逻辑分析☆☆☆7围棋的气逻辑分析☆☆☆8分割平衡字符串逻辑分析☆☆☆9机器人搬砖二分法☆☆☆10转盘寿司数据结构/栈/单调栈☆☆☆11小明找位置二分法☆☆☆12提取字符串的最长合法简单数学表达式双指[...]
[...]序号题目考点难易程度1二叉树计算二叉树前序、中序遍历☆☆☆25G网络建设最小生成树☆☆☆☆3找数字逻辑分析☆☆☆4符号运算数据结构 / 栈☆☆☆5爱吃蟠桃的孙悟空二分法☆☆☆6结队编程暴力枚举 二叉树索树☆☆☆7石头剪刀布游戏逻辑分析☆☆☆8攀登者2逻辑分析☆☆☆9分月饼递归☆☆☆10电脑病毒感染图论 / 单源最短路径(dijkstra☆☆☆[...]